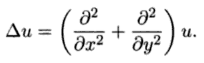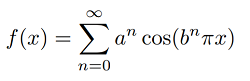Types of Functions: Contents:
What is a Function?
A function is a type of equation or formula that has exactly one output (y) for every input (x). If you put a “2” into the equation x2, there’s only one output: 4. Some formulas, like x = y2, are not types of functions, because there are two possibilities for output (one positive and one negative).
Note to Excel and TI graphing calculator users: A “function” is a predefined formula. All Excel built-in functions are also functions in the traditional sense (i.e. you’ll get one output for every input).
More on the difference between formulas and functions.
4 Types of Functions
Sometimes, functions are placed into different categories. For example, functions can be divided into four broad categories:
- Set elements: Classified according to how many relationships exist between the domain and codomain. For example, One to One function, many to one function, surjective function. constant function.
- Equations: Based on the polynomial degree. For example, linear function, cubic function.
- Range: Based on the outputs (aka range). Examples include inverse function, periodic functions, and sign function.
- Domain: Based on the types of equations used to define the functions. Includes algebraic functions, logarithmic functions, and trigonometric functions.
Function Notation
Function notation tells you that the equation you’re working with meets the definition of a function.
The most common function notation you’ll see is f(x), which is read aloud as “f of x”.
The “f(x)” is used in place of the “y” in a formula; They mean the exact same thing. For example, instead of the more familiar y = 2x, you’ll see f(x) = 2x. There’s no difference between the two formulas, other than the different notation.
Any letter can be used instead of f (see function names below). For example:
- g(x)
- h(x)
- z(x)
Examples
- y = 2x + 4; solve for y when x = 2.
- f(x) = 2x + 4; solve for f(x) when x = 2.
The two formulas above are telling you the same thing, they are solved in the same way (plug in your x-value and solve), and they give you the exact same solution:
- y = 2x + 4 = 2(2) + 4 = 4 + 4 = 8
- f(x) = 2x + 4 = 2(2) + 4 = 4 + 4 = 8
You might also see questions written like this:
f(x) = 2x + 4; solve for f(2)
This means the same thing as:
f(x) = 2x + 4; solve for f(x) when x = 2.
More examples: Evaluating a Function.
Why Use Function Notation?
So, if y and f(x) mean the same thing, why use function notation at all? It might seem arbitrary to use f(x) or g(x) instead of y, but it can help you separate different parts of a formula and work with them more easily. Function notation gives you more information, and more flexibility.
For example, the chain rule uses the function notation F′(x), f′(x), g(x) and g′(x). It tells you that those four parts need to be dealt with separately:
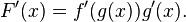
Let’s take out all the different notations and replace them with the more familiar “y”:
![]()
It certainly looks simpler, but good luck with trying to solve it!
Types of Functions: Names and Arguments
The function name is the letter that represents the function:
- g(x): The function name is “g”
- h(x): The function name is “h”
- z(x): The function name is “z”
The argument is the letter in parentheses. In all three of the above examples, the letter is “x”. You might also see “t” or any other letter:
- g(x): The argument is “x”
- h(t): The argument is “t”
- z(s): The argument is “s”
Types of Functions: How To Know if It’s a Function
The vertical line test is a simple way to figure out if you have a function.
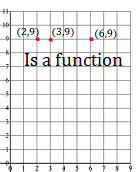
You could also use to “many to one” rule:
 Is a function: “many to one“. This is saying if you have multiple x-values that map to one y-value — say, (2,9), (3,9) and (6,9) — then that still qualifies as a function. Put more simply, it’s okay for a function to have multiple coordinate points in a straight line from left to right.
Is a function: “many to one“. This is saying if you have multiple x-values that map to one y-value — say, (2,9), (3,9) and (6,9) — then that still qualifies as a function. Put more simply, it’s okay for a function to have multiple coordinate points in a straight line from left to right. Not a function: “one to many“. In other words, let’s say you had one x-value that maps to many y-values. For example, — in coordinate notation — (2,1) and (2,10). If the first number (the x-value) repeats, then you do not have a function. To put that another way, if you have multiple coordinate points in a straight line up and down, then that’s not a function.
Not a function: “one to many“. In other words, let’s say you had one x-value that maps to many y-values. For example, — in coordinate notation — (2,1) and (2,10). If the first number (the x-value) repeats, then you do not have a function. To put that another way, if you have multiple coordinate points in a straight line up and down, then that’s not a function.
As a practical example of one to many, one person can have several children. However, one child can only have one biological mother (an example of a one to one relationship). To put this into a more mathematical context: Let’s suppose a set S of ordered pairs (x, y) represents the statement “x is the mother of y”. The set S is a one to many relationship, because multiple ordered pairs can have the same value for x (i.e. one mother x can have multiple children, y).
See also:
Issues with One to Many and Many to One
Although the above guidelines are found in many textbooks, they are deceptively complicated to use, because some graphs that have the “many to one” situation aren’t necessarily going to be functions; There may be other places (i.e. a couple of other coordinate points) that connect vertically, therefore disqualifying it as a function. These “rules” can also be difficult to remember (is it the first number that can repeat? Or the second?). Sometimes, it’s practically impossible to figure it out without some heavy algebra or the use of a computer. That’s because even if you have a few coordinates—or even an equation—you might be missing just a single point (perhaps with a very large x-value) that makes your graph not a function.
Why is this important?
You can’t do much with an equation in calculus if it isn’t a function. You could cut up a challenging function into smaller, function-like pieces (called piecewise functions), but in essence, calculus only works properly with functions. If you don’t perform a vertical line test before doing some calculus, then your solutions can be misleading or just plain wrong.
Properties of Functions
A function takes an input (x) and produces a single output (y) for each x-value. Functions also pass the vertical line test; if you draw a vertical line through the graph of a function, it never intersect the graph more than once.
Properties of Functions
All functions have certain properties, or distinct features, which can be very useful when trying to analyze them. The following common properties of functions describe how a graph is shaped, what happens as x-values increase, and whether the functions can be further analyzed with calculus:
- Domain and Range
- Even or Odd
- Increasing or Decreasing
- Maxima and Minima
- Concave Up or Down
- Bounded or Unbounded
- Continuous or Discontinuous
- Differentiable or Non-Differentiable
1. Domain and Range
The set of all inputs (e.g., x-values) is called the domain. For example, the f(x) = x2 can have any number as an x-value, so the domain is (-∞, ∞). The range is the set of all outputs (e.g., y-values).
See also: How to find the domain and range of a function.
2.Even or Odd

An even function.
Even functions have symmetry about the vertical axis: f(-x) = x for every x.
An odd function.
Odd functions have symmetry about the origin: f(-x) = x for every x in the domain.
Functions do not have to have even or odd symmetry: they can be neither.
More info and tests: Even and Odd Functions
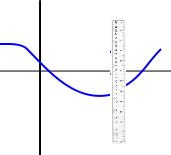
3.Increasing or Decreasing
Increasing functions travel upwards from left to right; as x increases, y decreases. With decreasing functions, as you move from left to right, the graph goes downward. In other words, as x increases, y decreases.
More info and formal definitions: Increasing and Decreasing Functions
4.Maxima and Minima
The lowest point on a graph is called the minima; the highest point on a graph is called the maxima. “Global means “the entire graph of the function” while “local” refers to “a small part of the graph”.

See:
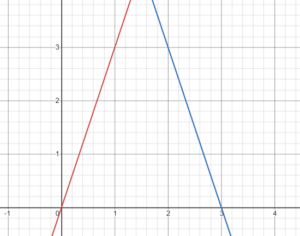
5.Concave Up or Down
Concavity tells you if a graph is shaped like the letter U (concave up) or an upside down U (concave down).
See: Concave up and down functions.
6. Bounded or Unbounded
Bounded functions have boundaries or constraints placed upon them. For example, if you were looking at a function describing car speed, you would be constrained by the speed limit of the car (perhaps 100 m.p.h.). Unbounded functions don’t have any constraints.
See: Bounded and unbounded functions.
7. Continuous or Discontinuous
Continuous functions have no breaks, jumps or holes. Otherwise, they are discontinuous. In calculus, we are most interested in those functions that are continuous, because discontinuity makes it challenging to analyze them.
See also:
8. Differentiable or Non-Differentiable
“Differentiable” means there is a slope that you can calculate. This slope will tell you something about the rate of change: how fast or slow an event (like acceleration) is happening.
The derivative must exist for every point in the domain, otherwise the function is not differentiable. This might happen when you have a hole in the graph: if there’s a hole, there’s no slope (there’s a dropoff!).
See: Differentiable vs. Non Differentiable Functions.
Types of Functions: References
Some graphs created with Desmos.
What is a Functional?
In general, a functional is a function of functions: a function that depends on other functions.
There are a few modifications on the basic definition. Which one you use depends on what field you’re working in.
Functionals: Different Definitions
1. Calculus of Variations
Functions, the building blocks of differential calculus, take scalars as inputs and produce scalars as outputs. Functionals are the building blocks for calculus of variations, taking a function as an input, returning a scalar output.
While there are different types of functionals, calculus of variations is mostly concerned with one in particular: where a definite integral’s integrand contains a (yet to be determined) function. The goal of calculus of variations is to study the changes in these functional while moving from one function to the next.
In notation, a functional is written as I[u(x)], where I is a unique scalar value for each function u(x). For example: [1].
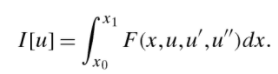
2. General Mathematics
In general mathematics, a functional may refer to a function specifically produced from a set of real-valued functions. For example, a functional could be the maximum of a set of functions on the closed interval [0, 1]. A binary functional takes two sets of functions to create one function. For example, the maximum of two sets of functions on the interval [0, 1]. The complement of a functional is a closure [2].
3. CompSci
Functionals in computer science (particularly machine learning) are defined slightly differently, as taking functions as arguments or yielding functions as results. Functionals can map functions to real numbers and real numbers to functions. In this context, they are often called higher-order functions. Higher-order functions include the differential operator and the definite integral. [3].
References
[1] Cassel, K. (2013). Variational Methods with Applications in Science and Engineering. Cambridge University Press.
[2] Watkins, The Calculus of Variations
in Functionals. Retrieved April 6, 2021 from: https://www.sjsu.edu/faculty/watkins/calcfunctionals.htm
[3] Harper, R. Functionals0. Retrieved April 6, 2021 from: https://www.cs.cmu.edu/~rwh/introsml/core/functionals.htm
Operations on Types of Functions
There are four operations on functions:
- Addition,
- Subtraction,
- Multiplication,
- Division.
For the purposes of the following examples, I’ll use functions f(x) and g(x).
You don’t have to use “f” and “g”. That notation is somewhat arbitrary. The functions could be represented by any letters; The choice depends largely on the preference of a particular author or professor. For example: j(t), s(t) or h(t). You might also see time(t) instead of “x”, especially in economics and physics applications.
Examples of Operations on Types of Functions
1. Addition
With addition, you can add together two or more functions. The formula is:
(f + g)(x) = f(x) + g(x)
Suppose we wanted to add the following two functions:
- f(x) = x2
- g(x) = 4x + 6
To get the solution, plug the functions into the formula:
(f + g)(x) = (x2) + (4x + 6) = x2 + 4x + 6
Combine like terms when possible. To illustrate, assume you want to add the following two functions:
- f(x) = 10x + 1
- g(x) = 12x – 3
- (f + g)(x) = (10x + 1) + (12x – 3) = 22x – 2
2. Subtraction
Two or more functions can also be subtracted. The formula is:
(f – g)(x) = f(x) – g(x)
I will use the same values for functions f(x) and g(x) as in my first example above.
(f – g)(x) = x2 – 4x + 6
3. Multiplication
To multiply two functions, use the following formula:
(f · g)(x) = f(x) · g(x)
Using the same values for f(x) and g(x) as above results in the following solution:
(f · g)(x) = (x2) · (4x + 6) = 4x3 + 6x2
4. Division
Two functions can also be divided. The formula for the division is:
(f/g)(x) = f(x)/g(x)
Plugging the values from the running example, you get:
(f/g)(x) = x2/4x + 6
When working with operations on functions, simply look at what the operation is telling you to do – whether that is an addition, subtraction, multiplication or division. Once you identify the operation solve by plugging the values of the functions into the above formulas.
You can find more example here: Combinations of Functions.
6. Types of Functions: A to Z
Obviously, this is a very long list. Either scroll down to find the type of function you want to learn more about, click a letter in the A-Z list below, or press Ctrl + F on your keyboard to search for specific types of functions. As an alternative, you can use the Google search box that’s embedded on the site (at the top right of the page). If you don’t see the function you need listed here, post a comment and I’ll add it!
Types of Functions from A to Z (Click on the function name for more information about the specific function):
Click to skip to that letter: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Click on the function name for more information about the specific function):
Types of Functions: A to O
- Abelian Functions
- Absolute Value Function
- Absolutely Continuous
- Absolutely Integrable Function (Summable Function)
- Accumulation Function
- Arcsin function
- Additive Function
- Affine Function
- Airy Function
- Almost Periodic Function, Quasiperiodic
- Aperiodic Function (Non Periodic)
- Area Function
- Arithmetic Functions
- Auxiliary Function
- Basis Functions
- Barnes G-Function
- Blancmange Function (Tagaki Curve)
- Barnes G-Function
- Bessel Function
- Beta Function / Incomplete Beta Function
- Bijective Function
- Bilinear Function
- Binomial Function
- Borel Function
- Broken Function
- Bounded Function
- Bounded Variation
- Boxcar Function
- Bump Function (Test Function)
- C0, C1, C2 Functions
- Ceiling Function
- Center Function (Triangle)
- Chi Function (Legendre’s Chi Function)
- Choice Function & The Axiom of Choice
- Clausen Function (Integral)
- Closed Function
- Cofunction
- Complementary Function
- Complex Function
- Composite Function
- Conjugate Function
- Constant Function
- Continuous Function
- Continuously-differentiable function
- Concave Function
- Convex Function
- Correlation Function
- Cosecant Function
- Cost Function
- Cotangent Function
- Covercosine Function (Coversed Cosine)
- Cubic Function
- Cumulative Distribution Function CDF
- Debye Function
- Decreasing Function
- Dedekind Eta Function
- Deterministic Function & Nondeterministic Function
- Digamma Function
- Dilogarithm Function
- Dirac’s Delta Function
- Dirichlet Function & Dirichlet Eta Function (Alternating Zeta Function)
- Discontinuous Function
- Displacement Function.
- Distance Function / Formula
- Divisor Function
- Elementary Functions
- Elliptic Function
- Empty Function
- Entire Function (Integral Function)
- Error Function
- Euler’s Totient Function / Phi Function
- Excosecant Function
- Explicit Function
- Exponential Function
- Exponential Integral Function
- Exsecant Functions
- Factorial Function
- Flat Function, Maximally Flat
- Floor Function
- Function of One Variable / Two Variables
- Gamma Function, Multivariate Gamma Function
- Gauge Function
- Generalized Function
- Gaussian Function
- Gauss Hypergeometric Function
- Gudermannian Function (Gudermann)
- H Function (Fox’s H-Function)
- Hankel Function.
- Harmonic Function
- Haversine Function
- Heaviside Function
- Holomorphic Function (Analytic Function)
- Homogeneous Function
- Hurwitz Zeta Function
- Hyperbolic Functions
- Hyperbolic Cosine Function
- Hyperbolic Sine Function
- Identical Function (Equal Function)!@!
- Identity Function
- Increasing Function
- Indicator Function
- Infinitely Differentiable Function
- Injective Function
- Inner Function
- Integrable Function
- Integrand Function
- Interpolation Function
- Interval Function (Interval-Valued Functions)
- Iterated Logarithm Function
- Into Function
- Inverse Cosecant Function
- Inverse Secant Function
- Inverse Cosine Function
- Inverse Functions
- Inverse Trigonometric Functions
- Lambert W function (Omega Function)
- Lebesgue Measurable Function
- Left-Continuous Function
- Legendre Function
- Lerch’s Transcendent
- Linear Functions
- Linear Parent Function
- Lipschitz Function
- Locally Integrable Function
- Logarithm function
- Logarithmic Integral Function
- Log Gamma Function
- Mapping Function
- Mathieu Functions: A Gentle Introduction
- Measurable Function: Overview
- Metric Function
- Möbius Function
- Modulo Function
- Meromorphic Function
- Meijer G-function
- Moment Generating Function MGF
- Monotonic Functions
- Multilinear Function
- Multivalued Function
- Many to One
- Monomial Function
- Named Function.
- Nearest Integer Function
- Non-Decreasing Function
- Non-Increasing Function
- Nonlinear Function
- Non Negative Function
- Normalized Function
- Nowhere Continuous Function
- Nowhere Differentiable Function
- nth Root Function
Types of Functions (O to Z)
Types of Functions: P to Z
- Path Function: Definition, Examples
- Parabolic Function
- Parametric Function
- Parent Function
- Partial Function
- Partition Function P, Q
- Pentation Function
- Periodic Function
- Piecewise Function
- Polar Function
- Polygamma Function
- Polynomial Functions
- Polylogarithm Function
- Power Functions
- Position Function
- Positive Function
- Popcorn Function (Thomae’s function)
- Prediction Function
- Probability Density Function
- Probit Function
- Production Function
- Prime Counting Function
- Probability Mass Function (PMF)
- Profit Function
- Point Function
- Pulse Function
- Ramp Function
- Rational Function
- Real Analytic Function
- Real Valued Function
- Reciprocal Function
- Rectangular Function
- Regularized Incomplete Beta Function
- Right Continuous Function
- Riemann Xi Function
- Riemann Zeta Function
- Revenue Function
- Sawtooth Function (Wave)
- Scalar Function
- Secant Function
- Septic Function (7th Degree Polynomial)
- Set Function
- Set-Valued Function
- Sextic Function
- Sigma Function
- Sign Function
- Simple function
- Sinc Function
- Sine Function
- Sine Integral Function
- Singularity Functions
- Sinusoidal Function
- Smooth Function
- Special Functions
- Square Function
- Square Integrable Function (Quadratically Integrable)
- Square Wave Function (Pulse Wave)
- Step Function
- Stochastic Function: Definition, Examples
- Struve Function
- Superadditive Function & Subadditive Function
- Surjective Function
- Tangent Function
- Target Function
- Tetration Function
- Total Function
- Transcendental Functions
- Triangle Wave Function
- Trigonometric Function
- Trinomial Function
- Unary Function
- Uniformly Continuous Function
- Univalent Functions
- Unit Ramp Function
- Univariate Function
- Universal Function
- Weakly Increasing Function
- Weierstrass Function
- Weight Function
- Weierstrass Functions
- Whittaker Function
types of Functions: Arithmetic Function
Contents:
What Are Arithmetic Functions?
An arithmetic function is any function from the set of natural numbers (whole, non-negative numbers that we use to count) to the set of complex numbers. In other words, it’s a complex-valued function that is defined on the set of natural numbers. In notation, that’s:
f: ℕ → ℂ
Arithmetic functions are mostly theoretical, used to investigate properties of natural numbers. As a general idea, you can think of an arithmetic function as a sequence of real numbers or complex numbers (although, as A.J. Hildebrand points out, looking at the functions in this way isn’t very useful).
Types of Functions: Examples of Arithmetic Functions
Arithmetic functions are primarily used in number theory, where they are sometimes called number-theoretic functions. Their behavior can be strange and difficult to predict, but some of the simpler and well known functions are very useful in number theory.
Two of the most important arithmetic functions are Euler’s totient function and the Möbius function. However, the functions don’t have to have proper names. For example, the following are all arithmetic functions (Wong, n.d.):
- The number of divisors of a certain number n,
- The number of primes less than n,
- The number of ways n can be represented as a sum of two squares.
Normal Order of an Arithmetic Function
Roughly speaking, an arithmetic function has the normal order F(n) if f(n) is approximately equal to F(n) for almost all values of n.
More precisely ((Hardy & Wright, 1979), the normal order of F(n) is f(n) if, for every positive ε and almost all values of n
![]()
Another way to put this (Porubský, 2020): a function f has normal order F if a set of positive integers S exists of asymptotic density 1 such that
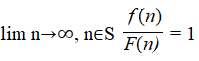
History of Normal Order
The concept was first introduced by Hardy and Ramunujan (1917, as cited in Indlekofer, 2001), where they proved that two arithmetical functions ω and Ω have the normal order “log log n”, where:
- ω(n) = the number of different prime divisors,
- Ω(n) = all prime divisors (counted with multiplicity).
Arithmetic Function: References
Hardy, G. and Ramanujan, S. The normal number of prime factors of a number n, Quart. Journ. Math.Oxford 40, 76-92 ( 1917).
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford University Press, p. 356, 1979.
Hildebrand, A. (2005). Introduction to Analytic Number Theory. Math 531 Lecture Notes, Fall 2005. Retrieved December 11, 2019 from:
https://faculty.math.illinois.edu/~hildebr/ant/main1.pdf
Indlekofer, K. Number Theory -Probabilistic, Heuristic, and Computational Approaches.Computers and Mathematics with Applications 43 (2002) 1035-1061.
Iwaniec, H. (2014). Lectures on the Riemann Zeta Function. American Mathematical Society.
Miller, S. & Takloo-Bigash. (2006). An Invitation to Modern Number Theory. Princeton University Press.
Porubský, S. Normal Order. Retrieved 2020/6/3 from Interactive Information Portal for Algorithmic Mathematics, Institute of Computer Science of the Czech Academy of Sciences, Prague, Czech Republic, web-page https://www.cs.cas.cz/portal/AlgoMath/NumberTheory/ArithmeticFunctions/NormalOrder.htm
Schachner, M. Algebraic and Analytic Properties of Arithmetic Functions. Retrieved December 11, 2019 from: http://math.uchicago.edu/~may/REU2018/REUPapers/Schachner.pdf
Wong, R. Average Values of Arithmetic Functions. Retrieved December 11, 2019 from: https://ocw.mit.edu/courses/mathematics/18-104-seminar-in-analysis-applications-to-number-theory-fall-2006/projects/wong.pdf
Types of Functions: Divisor Function
In calculus, when an author uses the term “divisor function”, it usually refers to a function by which another function is divided. However, there are specific types of divisor functions used mainly in number theory, including the Dirichlet and summatory divisor functions.
1. Divisor Function as a Divisor
In general mathematics, a “divisor” is defined as “…another number by which another number is to be divided” (Oxford). For example:
In 12 ÷ 4 = 3, 4 is the divisor.
This can be extended to function division in calculus. For example:
In f(g) ÷ f(h), f(h) is the divisor function.
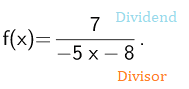
Dividing functions is something that crops up now and again in calculus, especially as it relates to defining functions.
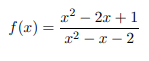
You’ll also see this type of function in the quotient rule:
Dirichlet and Summatory (Sigma) Divisor Function
In number theory, the Dirichlet divisor function is a count of how many positive divisors some number “n,” has, including n and 1.
For example:
- If n = 10, then d(10) = {1, 2, 5, 10} = 4.
- If n = 25, then d(25) = {1, 5, 25} = 3
The Dirichlet divisor function is sometimes denoted with (d(n)). However, this terminology may be confused with another function, which equals the sum of the positive divisors of n, including n and 1. This is sometimes referred to as the sigma function (not to be confused with the Weierstrass sigma function) or summatory divisor function to distinguish it from the Dirichlet. Note that the two divisors differ in that the Dirichlet version is a count of how many, while the summatory divisor function is a sum of all divisors.
While some authors specify that the function is Dirichlet or Summatory, others do not. Make sure you read the authors intent, rather than guessing the meaning.
Restricted Divisor Function
The restricted divisor function is defined as the sum of the divisors of n, excluding n. It is usually denoted as s(n).
Notation Notes
The divisor function can be denoted by d(n), ν(n), τ(n) or Ω(n).
Euler’s Totient Function
Euler’s Totient Function (also called the phi function) counts the totatives of n: positive integers less than or equal to n that are relatively prime to n. In other words, it’s the simple count of how many totatives are in the set {1, 2, 3, …, n}.
It is denoted by either φ(n) or Φ(n).
What are Totatives?
Totatives are positive integers smaller than a certain number n, but relatively prime to n. Two numbers are relatively prime if they one share “1” as a common factor.
Although Leonhard Euler invented the phi function, the word “totative” was coined by James Sylvester in 1879. It’s unclear why he chose that particular word; It’s likely he made it up from the Latin stem word tot, which means “so many” (Joyce, 2006) or perhaps as a combination of “total” and “quotient” (Turner, 2008).
How to Calculate The Phi Function
A simple (but a little tedious) way to perform the calculation by hand is:
- Write down all of the numbers in the set.
- Delete the numbers that share any common factor greater than 1.
As an example, let’s say the number in the set is n = 30.
Step 1: Write out the numbers:
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30}.
Step 2: Delete any numbers with factors greater than 1. The number 30 has the following factors: 1, 2, 3, 5, 6, 10, 15, 30.
- Starting with “2”, delete any multiples of two from the list, leaving:
{1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29}. - Next, delete any multiples of three from the list:
{1, 5, 7, 11, 13, 17, 19, 23, 25, 29}. - Then 5:
{1, 7, 11, 13, 17, 19, 23, 29}. - Then 6:
{1, 7, 11, 13, 17, 19, 23, 29}. - Next: 10:
{1, 7, 11, 13, 17, 19, 23, 29}. - Then: 15:
{1, 7, 11, 13, 17, 19, 23, 29}. - Finally: 30:
{1, 7, 11, 13, 17, 19, 23, 29}.
Euler’s totient for n = 30 is the last set (8).
You may notice that for the last few steps, the set remained unchanged. If you know your primes, you can slip a few steps by only testing primes less than or equal to the square root of n. The square root of 30 is 5.477, so you only actually need to test the numbers 2, 3, and 5.
Uses for Euler’s Totient
Euler’s totient function is an arithmetic function, which means that it draws from the set of real numbers and maps to the set of complex numbers. They are particularly useful for investigating properties of natural numbers, including primes.
Euler’s totient function has few real-life uses (for example, you probably won’t use one in applied science). However, one are where it is used is in public key cryptography.
References
Joyve, D. (2006). Math 126 Number Theory. Retrieved December 12, 2019 from: https://mathcs.clarku.edu/~djoyce/ma126/meeting18.pdf
Sylvester, J. (1879). On Certain Ternary Cubic Form Equations, Amer. J. Math. 2 pp 280-285, 357-393
Turner, C. (2008). Euler’s Totient Function and Public Key Cryptography. Retrieved December 12, 2019 from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.574.3949&rep=rep1&type=pdf
Harmonic Function
A harmonic function (called a potential function in physics) is a real-valued function with continuous second partial derivatives that satisfy the Laplace equation. The equation is satisfied when Δu = 0, where Δ is the Laplace operator.
The definition isn’t very intuitive to grasp, but it’s based on simple harmonic motion that up and down motion of a spring, which can be represented by sine functions and cosine functions. In multivariable calculus (i.e. in higher dimensions), that type of motion happens on the unit n-sphere, and is represented by the Laplace equation. That’s simplifying the definition a lot, but the definition itself isn’t meant to be enlightening; the harmonic function definition is just an equation—one that’s meant to be relatively easy to work with (Davis, 2016).
Simple Harmonic Motion
Simple harmonic motion is a special kind of repetitive back and forth movement. In simple harmonic motion, the movement is through a central position called the equilibrium, and the maximum displacement on one side of the equilibrium is the same as the maximum displacement on the other side.
The secret behind this type of motion is the force: the force which creates the motion is directed toward the equilibrium position and is always directly proportional to the distance from it. What this means is that the further we go from the equilibrium, the stronger the force that pulls us toward it.
Example of Simple Harmonic Motion
A basic example of simple harmonic motion is the way a spring, connected to a weight, would vibrate on a friction-less surface after being displaced by your hand.
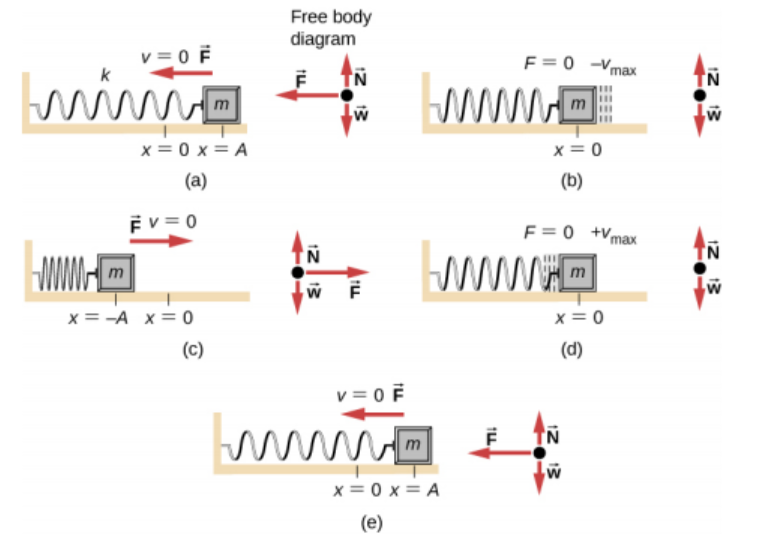
- Image a shows the spring when you have just pulled the object a distance of X and then released. The instantaneous velocity is 0, but the spring is exerting a force on the spring in an effort to get back to x = 0.
- In image b, the weight has reached the equilibrium and force is zero, but the velocity is at the highest it will be and it will carry the weight onward to the left.
The further the weight moves to the left, the greater the force to the right becomes. Eventually it cancels out the velocity, and the weight is sent back to the right, where it crosses the equilibrium with the same maximum velocity it just crossed it in the other direction. Since we have a friction-less system, the weight will return to the exact same place we pulled it to originally.
We call the time it takes to make a complete cycle the period T. The bigger our weight, the greater the time T. Also, the stiffer the spring, the smaller the time T.
Harmonic Function Examples
Harmonic functions are found in a wide variety of settings as diverse as animation, electric circuits, heat distribution and random walks. In physics, harmonic functions are determined by their singularities and boundary conditions (conditions that have to be satisfied at the boundary of a region where you’re solving a set of differential equations).
The real and imaginary parts of any holomorphic function are two-variable harmonic functions.
Formal Definition of a Harmonic Function
The formal definition of a harmonic function is (Greene & Krantz, 2006):
A real-valued function u: U → ℝ on an open set ∪ ⊆ ℂ is harmonic if it is C2 on U and Δu ≡0, where the operator Δu is Laplacian, defined as:
If you’re unfamiliar with mathematical/set notation:
- ℝ = the set of real numbers,
- ℂ = the set of complex numbers,
- ≡ = equivalent to,
- ⊆ = a subset of, or equal to,
- ∂ = partial derivative,
- C2 is a class of differentiable functions, where the first derivative and second derivative both exist, and are continuous.
References
Ash, J. M. (Ed.). Studies in Harmonic Analysis. Washington, DC: Math. Assoc. Amer., 1976.
Benedetto, J. J. Harmonic Analysis and Applications. Boca Raton, FL: CRC Press, 1996.
Cohn, H. Conformal Mapping on Riemann Surfaces. New York: Dover, 1980.
Davis, S. (2016). Voltage, Temperature, and Harmonic Functions. Retrieved January 10, 2020 from: Voltage, Temperature, and Harmonic Functions
Green, R. & Krantz, S. (2006). Function Theory of One Complex Variable. American Mathematical Society.
Krantz, S. G. “Harmonic Functions.” §1.4.1 and Ch. 7 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 16 and 89-101, 1999.
OpenStax. University Physics. 15.1. Simple Harmonic Motion. LibreTex Library, powered by MindTouch. Retrieved from https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_I_-_Mechanics%2C_Sound%2C_Oscillations%2C_and_Waves_(OpenStax)/15%3A_Oscillations/15.1%3A_Simple_Harmonic_Motion on August 17, 2019
OpenStaxCollege. College Physics. A Special Periodic Motion. Retrieved on August 17, 2019.
Images Provided by OpenStaxCollege, licensed under CCA 4.0
Lambert W function
Simply put, the Lambert W function is the inverse function of f(x) = xex.
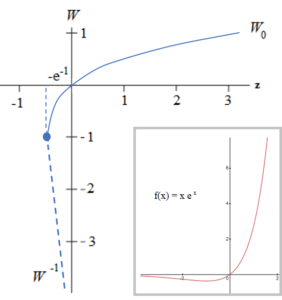
The graph above shows the real-valued branches for Lambert’s W. The graph is split into two parts (indicated by the blue dot at (-e-1, -1)), each of which share a tangent line.
- The blue line (W0) is the inverse of the function f(x) = xex with the function restricted to y-values ≥ -1. This is sometimes called the main branch because it goes through the origin.
- The rest of the function(W-1) curves in on itself (shown by the dashed blue line), creating multiple outputs for the same x-value. This part of the function violates the “each input maps to a single output” definition of a function.
The “piecewise” nature of the function is part of what makes Lambert’s W unusual and challenging to deal with.
Lambert’s W function, which can be real-valued or complex-valued, is a non elementary function used extensively in practically every scientific field including chemistry, computer science, mechanical engineering and physics. Its main purpose is to express solutions for equations where an unknown variable is present in an exponent and in another part of the equation.
Mathematical Definition
The Lambert W function can be defined mathematically as a solution to the following equation (Shynk, 2016):
x = w ew
The set of solutions are called branches. The domain of the function is (-e-1, ∞) and the range is (-∞, ∞).
A Challenging Function
Although the function is in widespread use, one of the major challenges with the Lambert W function is the lack of standard name and notation (Corless et al., 1996). As well as the fairly straightforward definition above, the function is defined in many different ways, including:
- “The multivalued inverse of the function w → wew” (Sanguin, 2013),
- “f(z) = zez, where ez is the exponential function, and z is any complex number” (Dobrushkin, n.d.).
Another challenge of using the function is that the variable “w” in the Lambert W function cannot be expressed as a function of x, even by taking the logarithm of both sides.
Finally, this unusual function has no symmetry. Therefore, it can’t be classified as either an odd or even function.
First Order Derivative Lambert Function
The first order Lambert W function is found by differentiating the functional equation defined above. When you do that, you get:
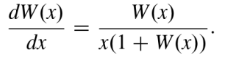
References
Corless, R. et al. (1996). On the Lambert W function. Advances in Computational Mathematics 5(1), 329-59.
Desmos Graphing Calculator.
Dobrushkin, V. MATHEMATICA TUTORIAL for the Second Course. Part I: Basic Matrix Operations.
Joyce, D. (2015). What is a simplified explanation of the Lambert W function?
Retrieved December 7, 2019 from: https://www.quora.com/What-is-a-simplified-explanation-of-the-Lambert-W-function
Pardalos, P. & Themistocles, R. (2016). Contributions in Mathematics and Engineering: In Honor of Constantin Carathéodory. Springer.
Sanguin, C. (2013). Computer Aided Assessment of Mathematics. OUP Oxford.
Shynk, J. (2016). Mathematical Foundations for Linear Circuits and Systems in Engineering. John Wiley & Sons.
Pardalos, P. & Themistocles, R. (2016). Contributions in Mathematics and Engineering: In Honor of Constantin Carathéodory. Springer.
Sanguin, C. (2013). Computer Aided Assessment of Mathematics. OUP Oxford.
Shynk, J. (2016). Mathematical Foundations for Linear Circuits and Systems in Engineering. John Wiley & Sons.
Lerch’s Transcendent
Lerch’s transcendent, named after Czech mathematician
Mathias Lerch (1860 – 1922) is defined by the power series [1]:
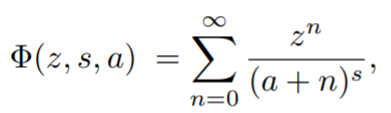
Where a ≠ 0, -1, -2, … on the domain |z| < 1 for any s ∈ ℂ or |z| ≤ 1 for ℝ > 1 [2].
Where Lerch’s Transcendent is Used
Many sums of reciprocal powers can be expressed in terms of Lerch’s transcendent function; It makes many appearances in physical science problems. For example:
- Formulation of electrostatic problems [3],
- Representation of distributions in particle physics. For example, in the Bose-Einstein Distribution (which describes the statistical behavior of bosons) [4].
- Production of urban noise maps [5].
In number theory, Lerch’s transcendent provides a unified framework for the study of many special functions. It can be obtained from the closely related Lerch zeta function by a change of variable z = e2πia [6]. Lerch’s functions are usually of interest because their analytic continuations include, as special cases, several important transcendental functions including the polylogarithm function and the Riemann zeta function [7]. Lerch’s transcendent generalizes the Hurwitz zeta function reducing to the Hurwitz zeta function when z = 1.
Lerch’s Transcendent: References
[1] Erdélyi, W. Magnus, F. Oberhettinger, and F. G. Tricomi (1953a) Higher Transcendental Functions. Vol. I. McGraw-Hill Book Company, Inc., New York-Toronto-London.
[2] Cai, X. & Lopez, J. (2021). A note on the asymptotic expansion of the Lerch’s transcendent. Retrieved April 24, 2021 from: http://arxiv-export-lb.library.cornell.edu/pdf/1806.01122
[3] Ivchenko, V. (2020). On the interaction force between a point charge and an infinite dielectric plate of finite thickness. European Journal of Physics, Volume 41, Issue 1, id.015201.
[4] Awan, A. (2015). On the Theory of Zeta-functions and L-functions. Retrieved April 24, 2021 from: https://stars.library.ucf.edu/cgi/viewcontent.cgi?article=1052&context=etd
[5] Lagarias, J. & Li, W. The Lerch zeta function III. Polylogarithms and special values. Retrieved April 24, 2021 from: https://ui.adsabs.harvard.edu/abs/2015arXiv150606161L/abstract
[6] Navas, L. (2015). The Lerch transcendent from the point of view of Fourier analysis. Journal of Mathematical Analysis and Applications.
[7] Wei, W. et al. (2015). Simplified analytical model for sound level prediction at shielded urban locations involving multiple diffraction and reflections. J Acoust Soc Am Nov;138(5):2744-58. doi: 10.1121/1.4932585.
Types of Functions: Metric Function
A metric space is a set taken together with a metric on that set. The “metric” is actually a function; one which defines the distance between any two members of the set. Often the members of metric space are called points; so we can say the metric defines the distance between any two points.
More formally, it is a set X, together with a metric function d, which assigns a real number (we can call this d(x,y)) to every pair x, y. There are some restrictions on what type of function we can call the ‘distance function’, so we’ll go through them below.
Properties of the Metric Function
A metric (our function d above) has to satisfy a few important properties, but they are all fairly simple and intuitive.
- If, and only if, x = y, then d(x,y) = 0.
- d(x, y) = d(y, x) (always)
- d(x, y) + d(y, z) ≥ g(x, z) (this is called the triangle inequality)
What these axioms tell us is that:
- The distance from a point to itself is always 1,
- A distance from one point to another is always the same as from the second point back, and
- The third side of a triangle is always less than the sum of its two sides (or equal, in the case that all points are on a straight line).
Examples of Metric Spaces
The metric space you may be most familiar with is the real numbers; there, the distance function is defined as d(x,y) = |y-x|.
Positive real numbers can also be defined as a metric space, with a distance function
d(x,y) = |log(y/x)|.
The set of all points on the floor in your room, with the distance between them defined as the measured distance in millimeters, is also a metric space.
Metric Space Circle Example
The more familiar way to define a circle’s metric space is through a Euclidean formula. Where it becomes more interesting is where you add different geometries, like Taxicab geometry, which requires you to get from a to b along a grid (much like how a taxicab might get from a to b in New York City).
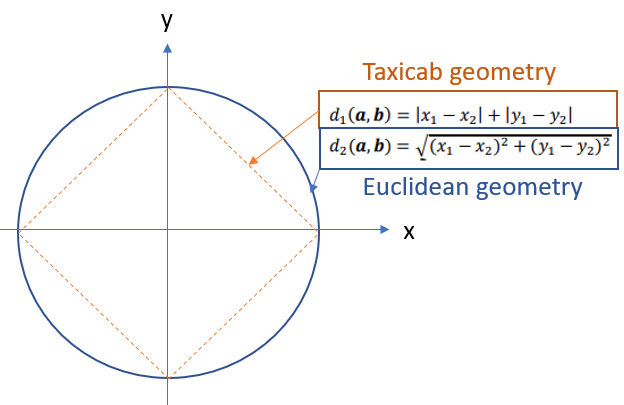
Types of Function: Named Function
In calculus, a “named function” refers to one of the following:
- A function that is fully defined
- A function that is familiar (i.e. it has a given name, like the Gamma Function).
- A function that is defined in mathematical software.
1. Fully Defined Types of Function
A named function sometimes means a function that is completely and fully defined, sometimes using logic. For example, Dijkstra & Scholten (2002) introduce the following named function in their book Predicate Calculus and Program Semantics:
“[f . Y ≡ Y]
with f, [according to an earlier definition], for any Z given by
[f . Y ≡ ¬ B ∧ P] ∨ (B ∧ wp. S . Z)]”
I’ve abbreviated the full definition here, because—because of previous definitions—the notation would take up half a post. But the point is, the authors left no stone unturned in fully defining the function.
Logic notation notes:
If you’re unfamiliar with logic symbols used above, here’s what they mean:
- ¬ is the negation symbol, which is sometimes written, equivalently, as ~.
- ∧ is the “logical and” symbol.
- ∨ is the “logical or” symbol.
2. Familiar Functions
The term named function is sometimes used simply to mean a function that is familiar and recognizable. Getting an “unfamiliar” function (one that doesn’t adhere to some kind of well-recognized format) into a “familiar” one (see: Types of functions for some examples) has many benefits. These include known derivatives, known integrals, and the ability to use software to manipulate the functions.
As an example, the following G-function appears on page 224 of Fractional Calculus and Its Applications: Proceedings of the International Conference held at the University of New Haven:
![]()
Although this is indeed labeled as a “G-Function”, it isn’t a “known” one. All that’s needed is to rewrite the expression in the brackets so that the function becomes a “named function.” This is similar to the idea of forcing expressions to be explicit functions, so that they can be manipulated algebraically.
Types of Functions: Named Functions in Software
In programming, named types of functions are defined by you, and depend on the data you’ve input into the software.
For example, let’s say you’ve input a list of children and those children’s mothers.
You might have a named function mother(x).
mother TINA results in JILL.
As another example, the following named function (sum-of-squares) takes two numbers as arguments and outputs the sum of their squares (Wailing, 2019):
(define sum-of-squares
(lambda (x y)
(+ (square x) (square y)))).
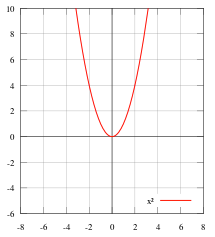
Types of Functions: The Square Function
Contents (Click to skip to that section):
1. Definition of Square Types of Functions
The square function squares all inputs. The formula is
f(x) = x2.
The graph (sometimes called a square map) is a parabola. The parabola is concave up (i.e. it looks like a cup). If you place a negative sign in front of the “x2” (not just the x-value), you’ll get an upside down parabola (i.e. one that is concave down).
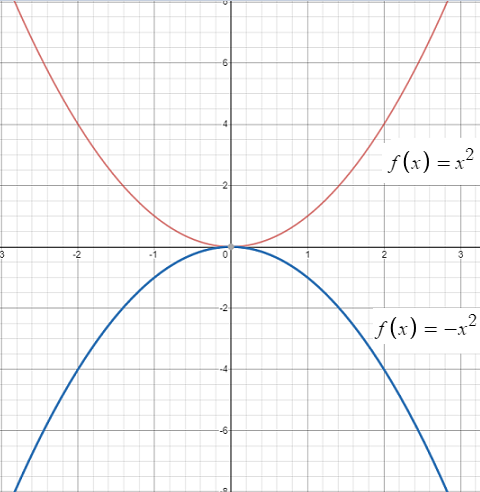
The square function only has one intercept: at the origin (i.e. x = 0).
The square function is the inverse of the square root function.
2. Domain and Range
The domain of the square function is the set of all real numbers. The range is the set of all non-negative reals, because squaring a number will always give a positive result.
The square function can also be defined in terms of its domain and range. It takes every real number in the domain, squares that number, and assigns it to the result in the range. The function gets its name because numbers are squared. For example if x = 4, then 42 = 16.
A few more examples of function values:
- f(0) = 0 * 0 = 0,
- f(2) = 2 * 2 = 0,
- f(-3) = -3 * -3 = 9,
- f(p) = p * p,
- f(height) = height * height.
3. Square Function Derivative
The square function derivative is 2x.

This uses the power rule to differentiate exponents. The steps for finding the derivative (shown in the above image) are:
- Copy the number of the exponent, and place it in front, so f(x) = x2 becomes f(x) = 2x2
- Subtract 1 from the exponent in the new equation from Step 1: f(x) = 2x2 – 1 = f(x) = 2x1 = 2x
Nearest Integer Function
The nearest integer function (also called nint or x-rounded) g(x) = {x} assigns the nearest integer to x for every real number. If x is in the middle of two integers, the function returns the largest of the two numbers (Gerstein, 2012), which avoids statistical bias (Nemati et al., 2013).
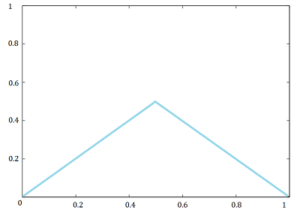
A few examples:
- {1.99} = 2,
- {6} = 6,
- {3.5} = 4,
- {-0.6} = -1,
- {-4.5} = -4.
The function is mostly used in number theory and approximation theory, with some application in dynamical system theory. It can also “tidy up a good many otherwise complicated formulas” such as the formula for the number of permutations of n letters with no fixed points:
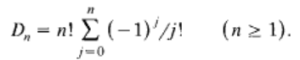
Which, when you realize that the sum is a truncation of the infinite series for e-1, simplifies to:
Dn = ||n!/e|| for n ≥ 1.
(Wilf, 1987, p. 855.).
Similar functions that belong to the same family — functions that return real integers based on a particular rule — include the ceiling (least integer) function and floor (greatest integer) function.
Notation for the Nearest Integer Function
The nearest integer function doesn’t have a commonly accepted standard notation. While it’s common to use curly brackets to represent the nearest integer function (as in the examples above), the symbol || || is also used; For example, ||0.49|| = 0 (Brown, 1998). Other notation includes the symbol “(x)” (Singh, 2021) and
Occasionally, brackets [] are used, but these can be confused with equivalence class. In addition, the floor function is sometimes denoted with brackets, especially in older texts, compounding the potential confusion. The notation |_x] is also sometimes used (Hastad et al. 1988), but this notation is cumbersome and not recommended (Nemati et al, 2013).
Nearest Integer Function: References
Brown, P. (1998). Advances in Chromatography – Volume 39 – Page 154. Taylor & Francis.
Gerstein, L. (2012). Introduction to Mathematical Structures and Proofs. Springer.
Hastad, J.; Just, B.; Lagarias, J. C.; and Schnorr, C. P. “Polynomial Time Algorithms for Finding Integer Relations among Real Numbers.” SIAM J. Comput. 18, 859-881, 1988.
Nemati et al., (2013). Using Black Holes Algorithm in Discrete Space by Nearest
Integer Function. IAES International Journal of Artificial Intelligence (IJ-AI)
Vol. 2, No. 4, December 2013, pp. 173~178.
Singh, S. (2021). 3.9 Greatest and least integer functions. Retrieved January 27, 2021 from: https://cnx.org/contents/[email protected]:p28zIztF@9/Greatest-and-least-integer-functions
Wilf, H. (1987). The Editor’s Corner: Strings, Substrings, and the `Nearest Integer’ Function. The American Mathematical Monthly Vol. 94, No. 9 (Nov., 1987), pp. 855-860 (6 pages) Published By: Taylor & Francis, Ltd.
Real Analytic Functions
Real analytic functions are locally given by a convergent power series (i.e. it has a power series on a particular neighborhood). More specifically, they can be expressed by a power series with non-empty radius of convergence—an interval of positive radius centered at α [1]: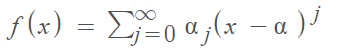
Real analytic functions are infinitely differentiable up to the nth derivative (e.g. first derivative, second derivative, third derivative,…).
Real Analytic Function Definition with Taylor Series
The power series expansion of an analytic function coincides with the Taylor series. This gives us another way to define a real analytic function, as one agrees with its Taylor series in a neighborhood of every point. In other words, a Taylor series will converge to the series at a certain point.
As an example, a function is real analytic at zero if there is some R > 0 so that:
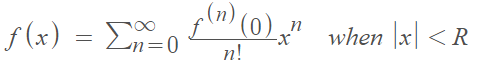
In order to be classified as real analytic, a function doesn’t have to agree with its Taylor series everywhere, just when R < 0.
More generally, these functions can be described as analytic at an arbitrary point a, in which case the expression would be differentiated at a:
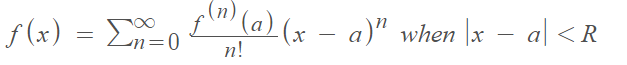
This tells that as long as |x – a| is less than R (i.e. we’re near point a), the function f can be written as a power series.
Properties of a Real Analytic Function
Real analytic functions are a very small class of functions within the set of smooth (infinitely differentiable) functions. In order to be classified as “real analytic”, a function must be all of the following:
- A real-numbered function,
- A continuous function,
- A differentiable function,
- A smooth function,
- In agreement with its Taylor series in a neighborhood of every point.
References
[1] Stefanski, R. (2004). Factorization of Polynomials and Real Analytic Functions. Retrieved July 8, 2021 from: https://radekstefanski.weebly.com/uploads/1/3/6/4/13643663/stefanski2004-factorization1.pdf
Types of Functions: Set-Valued Function
What is a Set-Valued Function?
In general, a set-valued function (also called a multi-valued function) has multiple inputs for a single output. In differential calculus of set-valued maps, the mapping is defined more precisely to include set-valued function derivatives.
Set-Valued Function: Simple Example
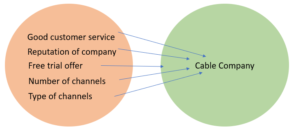
Let’s say a consumer wants to choose a cable TV service from a variety of similarly priced and affordable options. The consumer might be ambivalent about which to choose, and it may be difficult to pinpoint why they made that decision (includes sports channels? reputation of company?) but we know they will choose one. This multi-valued input to one output is the hallmark of a set-valued function.
A correspondence (from set theory) is an example of a set-valued function. A correspondence assigns a set of points to a single point; this set of points may be from the same set, or a different set entirely (Aliprantis & Border, 2006).
Fun fact: The longest name for a set-valued function is the Knaster-Kuratowski-Mazurkiewicz map, which maps from X to E, where (Beer, 1993):
- E is a locally convex space and
- X is a nonempty subset of E.
More Technical Definitions
For the most part, when you hear the term “set-valued function” it usually means it’s a multivalued function and the two terms are often used synonymously. However, there are more technical definitions that arise in areas such as differential calculus of set-valued maps. For example, Chalco-Cano et al. (2011) define a set-valued function as follows:
“A set-valued function is a function with values in Kn or KnC [Kn is the family of all nonempty compact subsets of ℝn and KnC is the family of all A ∈ Kn such that A is a convex set], the space of all nonempty compact subsets of Rn (the space of all nonempty compact convex subsets of Rn)”
Defined in this manner, it is possible to find derivatives for set-valued functions. These relatively new developments include H-differentiability (Banks et al., 1970; Hukuhara, 1967), G-differentiability (Chalco-Cano et al., 2008) and gH-differentiability (Stefanini and Bede, 2009).
Set-Valued Function: References
Aliprantis, C. & Border, K. (2006). Infinite Dimensional Analysis. A Hitchhiker’s Guide. Springer Berlin Heidelberg.
Banks, H et al. (1970). A differential calculus for multifunctions, Journal of Mathematical Analysis and Applications 29 (1970) 246–272.
Beer, G. (1993). Topologies on Closed and Closed Convex Sets. Springer, Netherlands.
Chalco-Cano, Y. et al. (2008). On the new solution of fuzzy differential equations, Chaos, Solitons & Fractals 38 (2008) 112–119.
Chalco-Cano, Y. et al. (2011). Generalized derivative and pi-derivative for set-valued functions q. Information Sciences 181 (2011) 2177-2188.
Hukuhara, M. (1967). Integration des applications mesurables dont la valeur est un compact convexe, Funkcialaj Ekvacioj 10. 205–223.
Stefanini, L. & Bede, B. (2009). Generalized Hukuhara differentiability of interval-valued functions and interval differential equations, Nonlinear Analysis 71 1311–1328
Walker, M. (2020). Correspondences. Retrieved October 20, 2020 from: http://www.u.arizona.edu/~mwalker/02_Equilibrium%20Existence/Correspondences.pdf
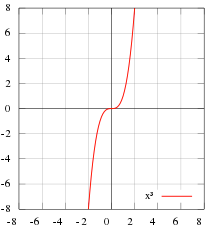
Sextic function
A sextic function (sometimes called a hexic function) is a 6th degree polynomial function. In other words, it’s a polynomial where the highest degree (i.e. exponent) is 6.
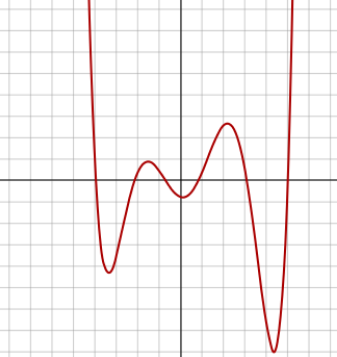
The general form:
f(x) = x6 + a5x5 + a4x4 + a3x3 + a2x2 + a1x + a0
Where the coefficients a, b, c, d, e, f, g are usually integers, rational numbers, real numbers or complex numbers.
Zeros of the Sextic Function
A sextic function can have between zero and 6 real roots/zeros (places where the function crosses the x-axis). These zeros can be difficult to find. In fact, roots of polynomials greater than 4 degrees (quartic equations) are notoriously hard to find analytically. Abel and Galois (as cited in Shebl) demonstrated that anything above a 4th degree polynomial can’t be solved with radicals; general sextics can be solved with Kampe de Feriet functions.
In theory, graphing the sextic function might be easier, but graphing can be equally challenging. This graph of the sextic function at Desmos.com has sliders so that you can experiment with different coefficients. You’ll notice though, that the graph is somewhat pathological, and honing in on the right window (so that you can see the entire graph) is a challenge in itself.
Derivative of a Sextic Function
The first derivative of a sextic function is a quintic function.
Sextic Equation
A sextic equation has almost the same notation as the general form of the sextic function, except that, instead of being presented with function notation, the formula is set equal to zero:
x6 + a5x5 + a4x4 + a3x3 + a2x2 + a1x + a0 = 0
References
Coble, A. (1911). The Reduction of the Sextic Equation to the Valentiner Form–Problem. Math. Ann. 70, 337-350.
Function graph: Krishnavedala [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)]
Types of Functions: Unary Function
A unary function has one input and one output. For example, the basic function f(x)is a unary function. This class of functions is the one most commonly studied in general math and calculus, so most of the types of functions you deal with in beginning calculus are unary.
The term unary is usually implied; when you hear reference to “a function,” it usually means a unary function. Other functions are referred to by their specific name to distinguish them from ordinary (unary) functions. For example, binary function or empty function.
Unary real functions take one argument and have a domain of real numbers. The ramp function is an example.
Unary Function in Set Theory and CS
In set theory, you can think of a unary function f as one which, when applied to an argument x, results in a juxtaposition of the two, as in f(x) (Tarksy & Givant, 1987). A unary function can also be thought in more simple terms as just a function that maps element of A to elements of A. A related term is a unary operation, which is defined on set A as A → A.
In computer science, unary functions act in the same way, except they are defined as function objects called with a single argument. In functional programming, these functions are also called monadic functions.
Use in Lambda Calculus
In lambda calculus, a purely theoretical form of calculus, every value is a unary function. Lambda calculus is a simple way of applying types of functions to arguments.
Weierstrass function
The term Weierstrass function may refer to either
- A specific continuous function without a defined derivative, or
- A special function of a complex variable.
1. “Nowhere Differentiable” Weierstrass Function
Weierstrass Functions are famous because they are continuous everywhere, yet nowhere differentiable. In general, they are extremely “bumpy”, which leads to problems with finding derivatives at any point.
In notation, the Weierstrass function (Weierstrass, 1872 as cited in Nelson) is defined as:
“Let a ∈ (0, 1) and let b be an odd integer such that ab < 1 + 3π/2. Then the
series
converges uniformly on ℝ and defines a continuous but nowhere differentiable function.”
A and B can be any numbers as long as:
- B is between 0 and 1, and
- A * B is larger than 1 + (3 * π/2), which is roughly equivalent to 5.71.
For example A = 12, B = 0.75.
Graph of the Weierstrass Function
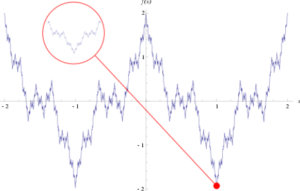
Theoretically, you could zoom in forever, and the function would never smooth out enough for the slope of the curve to be calculated.
2. Weierstrass Special Function
The Weierstrass Elliptic Function is found in complex analysis, and is a subtype of Elliptic functions, which are classified as either Jacobi or Weierstrass. The difference between the two is that the Weierstrass type has a second order pole at z = 0.
Some variants of the Weierstrass Elliptic Function include the Weierstrass sigma, zeta, eta and ℘-Function (also called the Weierstrass sigma function). The variants are closely related to each other, in the same way that sine function, cotangent function, and squared cosecant functions are related: the logarithmic derivative of the sine function is the cotangent function, whose derivative is the negative squared cosecant function.
Weierstrass function: References
Falconer, K. Fractal Geometry: Mathematical Foundations and Applications. New York: Wiley, 1990.
Hairer, E. and Wanner, G. Analysis by Its History. New York: Springer-Verlag, 1996.
Hardy, G. H. “Weierstrass’s Non-Differentiable Function.” Trans. Amer. Math. Soc. 17, 301-325, 1916.
Havil, J. “Weierstrass Function.” §D.2, Appendix D, in Gamma: Exploring Euler’s Constant. Princeton, NJ: Princeton University Press, pp. 230-231, 2003
Nelson, B, The Weierstrass Function. Retrieved December 31, 2019 from: https://math.berkeley.edu/~brent/files/104_weierstrass.pdf
Pickover, C. A. Keys to Infinity. New York: Wiley, p. 190, 1995.
Salzer, H. E. and Levine, N. “Table of a Weierstrass Continuous Non-Differentiable Function.” Math. Comput. 15, 120-130, 1961.
Singh, A. N. The Theory and Construction of Non-Differentiable Functions. Lucknow: Newul Kishore Press, 1935.
Types of Functions: References
Desmos Graphing Calculator.
Albert, John. Course Notes on Additivity. Retrieved from http://math.ou.edu/~jalbert/courses/additive_functions_2.pdf on June 14, 2019.Buchman, A. & Zimmerman, R. (1970). Eleventh Year Mathematics. Retrieved September 24, 2017 from: http://files.eric.ed.gov/fulltext/ED046731.pdf
Clarke, E. Lecture 5: Predicate Calculus. Retrieved April 7, 2020 from: http://www.cs.cmu.edu/~emc/15-398/lectures/lecture5.pdf
Tarsky, A. & Givant, S. (1987). A Formalization of Set Theory Without Variables, Volume 41. American Mathematical Association.
Edsger W. Dijkstra, Carel S. Scholten. (2012). Predicate Calculus and Program Semantics. Springer Science & Business Media.
Oxford Lexico, Retrieved November 30, 2019 from: https://www.lexico.com/en/definition/divisor
Kimblerling, C. (2020). Encyclopedia of Triangle Centers. Retrieved September 4, 2020 from: https://faculty.evansville.edu/ck6/encyclopedia/ETC.html
Reinhart, C. et al. Triangle Centers. Retrieved September4, 2020 from: https://brightspace.uakron.edu/d2l/common/viewFile.d2lfile/Database/MTQzMzU4MQ/Presentation_Group6_Reinhart_Kuzas_Burke.pptx?ou=6605&contextId=14871,13579
Ross, B. (Ed.). (2006). Fractional Calculus and Its Applications: Proceedings of the International Conference held at the University of New Haven. Springer.
Shapiro, Harold N. Introduction to the Theory of Numbers. Page 70. Retrieved from https://books.google.mn/books?id=4aX9WH8Kw_MC on June 3, 2019.
Shirali, S. First Steps in Number Theory: A Primer on Divisibility
Thompson, S. & Gardner, M. (1914). Calculus Made Easy, 2nd Edition. The Macmillan Company.
Young, C. (2018). Precalculus, 3rd edition. Wiley.
Wailing, F. (2019) Session 5: Racket Functions. Retrieved December 3, 2019 from: https://www.cs.uni.edu/~wallingf/teaching/cs3540/sessions/session05.html
Calculus of a Single Variable
Wenpang, Z. (2009). Proceedings of the Fifth International Conference on Number Theory and Smarandache Notions (Shangluo University, China). Infinite Study.
Zhang, W. (2005). Research on Smarandache Problems in Number Theory (collected …, Volume 2.
Whittaker Function
When Whittaker (1903) introduced his Whittaker function, he wrote it in terms of the closely related confluent hypergeometric function (Pearson et al., 2014; Ghayasuddin & Khan, 2017):
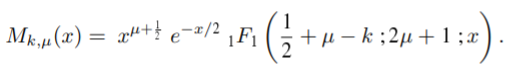
The function is therefore sometimes called the confluent hypergeometric function, but it could more correctly described as a modification of those functions. Whittaker’s purpose in formulating the new function was to make formulas more symmetric.
If you’re interested, Whittaker’s original 1903 text is freely available via Project Euclid (downloadable PDF).
Use of Whittaker Functions
The Whittaker function is a solution to the differential equation 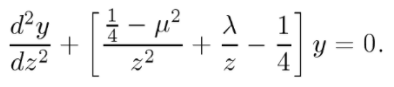
(White, 2010).
In mathematical physics, many functions are special cases of Whittaker functions, including error functions and the incomplete gamma function (White, 2010). Specific types include:
- Jacquet’s Whittaker functions: Generalized Whittaker functions of reductive groups over local fields,
- Kostant’s Whittaker functions: common eigenfunctions of Toda lattice Hamiltonians (Kostant, 1978).
In representation theory (which is, roughly speaking, the study of symmetry in linear spaces), the Whittaker function is well-studied example of a matrix coefficient of complex representations of p-adic algebraic groups. These appear in places like the integral expressions used to construct automorphic L-functions (Grodzicki, 2020). If you’re comfortable with representation theory of GLn(C), Dhillon’s The Models of Whittaker and Kirillov (PDF) is a good read on why you would want to consider Whittaker models.
References
Dhillon, G. (2017). The Models of Whittaker and Kirillov. Retrieved September 26, 2020 from: http://virtualmath1.stanford.edu/~conrad/conversesem/Notes/L6.pdf
Ghayasuddin, M. & Khan, N. (2017). Some Transformations and Generating Relations of Multivariables Hypergeometric Functions. Palestine Journal of Mathematics. Vol 6 (Special Issue II).
Grodzicki, W. (2020). Wellesley College Bio: https://www.wellesley.edu/math/faculty/grodzickiw
Kostant, B. (1978). On Whittaker vectors and representation theory. Inventiones mathematicae volume 48, pages 101–184. Springer.
Pearson, J. et al., (2014). Numerical Methods for the Computation of the Confluent and Gauss Hypergeometric Functions.
White, R. (2010). Asymptotic Analysis of Differential Equations. Imperial College Press.
Whittaker, E. (1903). An expression of certain known function as generalized hypergeometric functions, Bull. Amer. Math. Soc, 10 (1903), 125-134
 Is a function: “
Is a function: “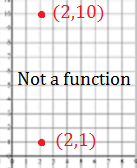 Not a function: “one to many“. In other words, let’s say you had one x-value that maps to many y-values. For example, — in coordinate notation — (2,1) and (2,10). If the first number (the x-value) repeats, then you do not have a function. To put that another way, if you have multiple coordinate points in a straight line up and down, then that’s not a function.
Not a function: “one to many“. In other words, let’s say you had one x-value that maps to many y-values. For example, — in coordinate notation — (2,1) and (2,10). If the first number (the x-value) repeats, then you do not have a function. To put that another way, if you have multiple coordinate points in a straight line up and down, then that’s not a function.