The term broken function has several meanings in calculus.
- The quotient of two functions.
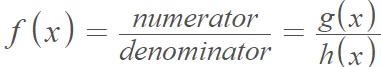
As this is a ratio, the denominator cannot be zero [1]. - The term “broken function” may also be used less formally to describe ill-behaved functions like the Weierstrass function, which is nowhere differentiable [2].
- The term is sometimes used as a synonym for piecewise functions (which are, literally, functions that are broken into pieces). An example is this article on satellite galaxies, where a broken function is characterized by a break splitting constant values with increasing linearity for a four-parameter function.
- In partial fraction decomposition, functions are broken into pieces before integrating. This makes some complicated functions easier to integrate.
- Colloquially speaking, a broken function may also refer to a function with holes.
“Old Math also allowed grimy, dirty tampering with functions saying that y = x is a function, but also, saying that at x = 0 then y = 3, and y = x elsewhere. What I called a broken function” ~ AP [3].
In computer science, the term can be used to describe a programming function (i.e., a block of code that is intended to perform an action) that doesn’t work.
Broken Function Space
A broken function space (or polynomial space) is a special case of broken Sobolev spaces.
For Sh ∈ {Kh, Ph) and integer k &gr; 0 they are defined by [4]
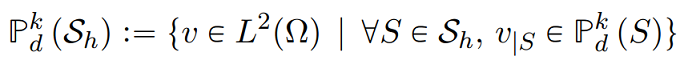
Where Pkd are the space of polynomial functions of, at most, degree k.
References
[1] Chapter 2: Functions of One Variable, Part 2. Retrieved March 6, 2022 from: https://www.studeersnel.nl/nl/document/maastricht-university/quantitative-methods-i/math-chapter-2-summary/5533756
[2] Lambert, F. Fractal zooms and infinite spaces: the Unbearable Quest for the Sublime. Retrieved March 6, 2022 from: https://www.academia.edu/12634007/Fractal_Zooms_and_Infinite_Spaces_the_Unbearable_Quest_for_the_Sublime
[3] Fibonacci sequence and now the AP subset sequence 0, 2, 5, 9, 14, 20, 27, 35, 44, 54, . . Retrieved March 6, 2022 from: https://groups.google.com/g/sci.math/c/iZi1o1dUksA?pli=1
[4] Pietro, D. & Lemaire, S. (2013). An extension of the Crouzeix–Raviart space to general mesheswith application to quasi-incompressible linear elasticity and Stokes flow. Mathematics of Computation from here https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.397.2235&rep=rep1&type=pdf