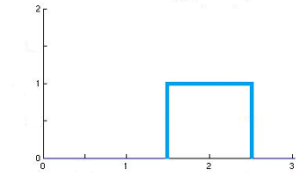
The pulse function, actually a family of functions, is particularly useful for representing physical quantities and as inputs for systems. It is widely used in signal processing and communications, where it is fundamental to understanding and working with those systems. It has a value of zero everywhere except for a specified, finite region.
One way to look at the pulse function is as a positive step function, followed by (or preceded by) a negative step function of equal magnitude at a later time.
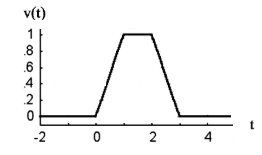
Although the function is usually associated with a rectangular shape, it isn’t limited to a rectangle: several other forms exist including the triangular and trapezoid pulse functions and even three-dimensional pulse functions. Which shape you use depends upon the variation you’re trying to describe.
When rectangular, the pulse function is sometimes also called the rectangle function, rectangular pulse function, box function or top-hat function.
Formal Definition of a Pulse Function
Formally, the function is defined as follows (Larson, 2011):
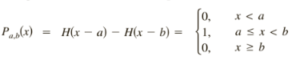
Where:
- a, b are positive numbers,
 is the heaviside function
is the heaviside function
In signal processing, the function is a result of on-off switching in a circuit.
Real Life Example
Cohan & Cole (2002) used a pulse function to model the effect of natural disasters on major family transitions. For the years 1975-1989, there were no natural disasters in the area being studied (South Carolina), so the function was given a value of zero. In 1989, the area was hit by Hurricane Hugo, so 1990 was given a value of 1. The following years (1991 to 1997) was given a value of zero. As an aside, an interesting conclusion in the study was that elevated births, marriages, and divorces were seen during the positive part of the function (1990).
References
Cohan, C. & Cole, S. (2002). Life course transitions and natural disaster. Marriage, birth and divorce following Hurricane Hugo. Journal of Family Psychology. 16, 16-25.
Larson, R. (2011). Calculus I with Precalculus. Cengage Learning.
Tang, K. (2007). Mathematical Methods for Engineers and Scientists 3: Fourier Analysis, Partial Differential Equations and Variational Methods. Springer Science & Business Media.
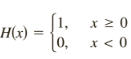 is the heaviside function
is the heaviside function