Partition Function P, Q: Simple Definition, Examples

Types of Functions >

Contents:
Partition Function in Mathematics
Use in Statistical Mechanics

Partition Function in Mathematics

There are two partition functions in math:

1. P (unrestricted)
2. Q (restricted).

1. P (Unrestricted)

P tells you how many ways you can write an integer as a sum of positive integers. For example, you can write the number 5 as:

• 5
• 4 + 1
• 3 + 1 + 1
• 3 + 2
• 2 + 2 + 1
• 2 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1

The number of partitions in the above example is written as P(5) = 7·(n).

Which order the summands (i.e. the quantities being added) are written in doesn’t matter. For example, 3 + 2 is the same as 2 + 3. However, the partitions are traditionally ordered from largest to smallest (Skiena, 1990, p. 51).

You can find a list of numbers and their partitions at the Online Encyclopedia of Integer Sequences. The first dozen (for integers 0 through 12) are:
1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56.

An exact formula for p(n) is given by Rademacher’s convergent series formula, which surprisingly (given its complexity!) gives p(n) for any integer greater than or equal to 1:


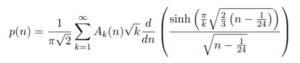
Where:


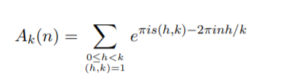
and s(h, k) is a Dedekind sum:

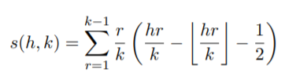
2. Q (Restricted)

The partition function Q is very similar, except that the numbers in each partition have to be unique. For example, the partition {2 + 2 + 1} in the above example would not count. In fact, the only partitions that would count are:

• 5
• 4 + 1
• 3 + 2

OEIS also has a list of the number of distinct partitions, the first dozen of which are: 1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, 12.

Partition Function in Statistical Mechanics

Every significant macroscopic quantity in a system can be expressed by a partition function. It’s a measure of how particles are spread out (i.e. partitioned among) energy levels in a system.

The partition function can be simply stated as the following ratio:

Q = N / N₀

Where:

• N = the total number of particles in a system,
• N₀ = the number of particles in the ground state.

The value for the ratio varies from 1 (the lowest value, when the temperature of the system is 0 degrees K) to extremely high values for very high temperature and where the spacing between every levels is tiny.

The Boltzmann Population Formula

The partition function has its origins in the Boltzmann Population formula, found in statistical mechanics:

Q = Σ_{j ωj exp (-Ej /kT}

can be found as the denominator in the Boltzmann population formula, which expresses the probability of finding a system in a particular quantum state, j:

P_j = ω_j exp(- E_j / kT) / Q

Where:

• E_j = energy of the quantum state,
• T = temperature in K,
• ω_j = degeneracy of the jth state,
• Q = the partition function.

The partition function can be written in various other ways, such as the sum of terms seen here:

References

Apostol, T. M. “Rademacher’s Series for the Partition Function.” Ch. 5 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 94-112, 1997.
Ault, A. (2008). The Partition Function: If That’s What It Is Why Don’t They Say So!
December 23, 2019 from: https://people.cornellcollege.edu/aault/Chemistry/PartitionFunction1.pdf
Calkin et. al. (2006). Computing the integer partition function. Retrieved December 23, 2019 from: http://www.math.clemson.edu/~kevja/PAPERS/ComputingPartitions-MathComp.pdf
Oldham, K. et al. (2010). An Atlas of Functions. Springer.
Chapter 7: Statistical Mechanics.
Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, 1990.