Probability and Statistics > Markov’s Inequality gives an upper bound on the probability that a non negative random variable is greater than or equal to some positive constant.
Given a non-negative random variable 
and a positive constant 
, Markov’s Inequality states that the probability that is greater than or equal to must be less than the Expected Value of divided by .
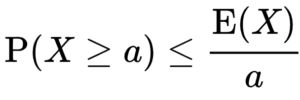
Markov’s Inequality is often expressed in a slightly different form, with the constant  being some multiple 
 of the Expected Value of .
Substituting 
 
 we get:
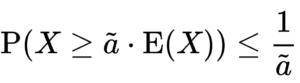
With this more familiar form we can look at an interesting and useful application of Markov’s Inequality.
Suppose we wanted to know, what percentage of people make more than 4 times the average income?
Here our non-negative random variable is income (all income is positive) and the Expected Value of is the same as the average income 
, assuming the income distribution is symmetric about the average income.
Substituting 
 and  we get:
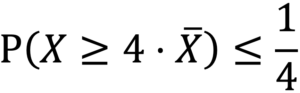
No more than 1/4 of the population (25%) can make more than 4 times the average income.
Intuitively it makes sense that there must be an upper bound for the percentage of people making more than 4 times the average income. If this number were too high (say 80%) the average income itself would be much higher than what it is.
Markov’s Inequality allows us to calculate this upper bound exactly, with the surprisingly simple result that the upper bound is just the reciprocal of the multiple of the average:
- no more than 1/3 of the population can make more than 3Â times the average
- no more than 1/5 of the population can make more than 5Â times the average
- no more than 1/10 of the population can make more than 10Â times the average
- etc…