A Borel function (or Baire function) is defined as a function where
{t: f(t) < a} ∈ B(ℝn)
for every a ∈ ℝ.
To define this slightly differently, if a function is Borel measurable, then that function is a Borel function. Measurable functions are, generally speaking, a generalization of the idea of continuous functions.
Borel Function Properties
A single-variable, real-valued Borel function has a domain and range on the real number line; these functions are measurable with respect to Borel sets.
Borel sets are certain subsets of topological space, which form the Borel σ-algebra of the space. Given a topological space X, there is a σ-algerbra on space X generated by open subsets of X. Borel sets are elements of this σ-algebra [1].
Therefore, the inverse image (i.e., the set of points that map to a given point) of any Borel set in the range space is a Borel set in the domain space [2]. Every real-valued continuous function is a Borel function. A complex-valued function is a Borel if both its imaginary and real parts are Borel functions [3]. We can generalize these statements to define Borel functions as any real-valued function or complex-valued function that has a Borel set as an inverse image f-1 for every open subset U of ℝ or ℂ [4].
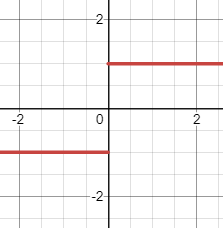
A simple Borel function is a step function; Borel functions are step functions or limits of step functions.
Given a Borel function, every pointwise limit is also a Borel function, so is every:
- Countable infinimum and countable supremum.
- Every countable limit inferior and limit superior.
- Bounded pointwise limit of a continuous function (for example, the indicator function) [4].
Every Borel function is Lebesgue measurable [5], but the converse is not true; In other words, Lebesgue measurable functions are defined in a larger set.
References
[1] Pfeiffer, P. (2013). Concepts of Probability Theory: Second Revised Edition. Dover Publications.
[2] Wan, K. (2019). Quantum Mechanics. A Fundamental Approach. Jenny Stanford Publishing.
[3] Bhat, B. Modern Probability Theory. New Age International.
[4] Sternberg, S. (2019). A Mathematical Companion to Quantum Mechanics. Dover Publications.
[5] Swartz, C. (1994). Measure, Integration and Function Spaces. World Scientific.