The blancmange function (also called the Tagaki function or curve) is a bumpy, pudding-shaped, nowhere differentiable function.
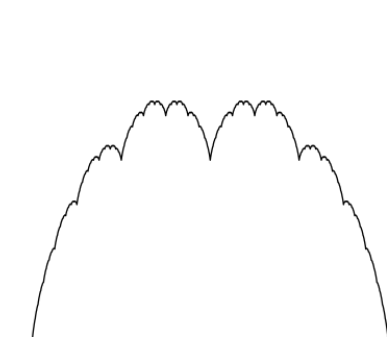
Originally called the Tagaki function, after its creator, it was renamed the blancmange function by Tall (1982).
Notation for the Blancmange Function
The blancmange function is defined as the infinite series (Kearnes, n.d.):
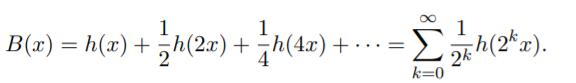
Where h(x) = inf{|x−n| | n ∈ ℤ} is a sawtooth function of period 1.
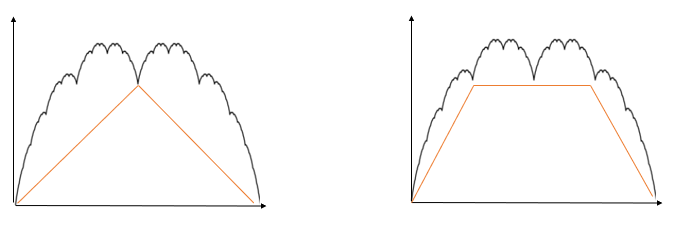
In simpler terms, the blancmange function is like a fractal, made up of an infinite number of smaller “blancmanges.” It can be constructed by adding up sawtooth function iterations to infinity (Tall, 2013).
References
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, pp. 111-113, 2007.
Dixon, R. Mathographics. New York: Dover, pp. 175-176 and 210, 1991.
Kearnes, K. The blancmange function. https://math.colorado.edu/~kearnes/Teaching/Courses/F18/Blancmange.pdfeitgen, H.-O. and Saupe, D. (Eds.). “Midpoint Displacement and Systematic Fractals: The Takagi Fractal Curve, Its Kin, and the Related Systems.” §A.1.2 in The Science of Fractal Images. New York: Springer-Verlag, pp. 246-248, 1988.
Tall, D. The Blancmange F. Continuous Everywhere but Differentiable Nowhere. The Mathematical Gazette. 66. 10.2307/3617301.
Tall, D. How Humans Learn to Think Mathematically: Exploring the Three Worlds of Mathematics. Cambridge University Press, 2013.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 16-17, 1991.