Contents:
- Definition of Differentiable
- Continuously Differentiable
- Infinitely Differentiable
- Non Differentiable Functions
- Nowhere Differentiable
What is Differentiable?
Differentiable means that a function has a derivative. In simple terms, it means there is a slope (one that you can calculate). This slope will tell you something about the rate of change: how fast or slow an event (like acceleration) is happening.
The derivative must exist for all points in the domain, otherwise the function is not differentiable. This might happen when you have a hole in the graph: if there’s a hole, there’s no slope (there’s a drop off!).
Continuously Differentiable
A continuously differentiable function is a function that has a continuous function for a derivative.
In calculus, the ideal function to work with is the (usually) well-behaved continuously differentiable function. If you have a function that has breaks in the continuity of the derivative, these can behave in strange and unpredictable ways, making them challenging or impossible to work with.
Formal Definition
More formally, a function f: (a, b) → ℝ is continuously differentiable on (a, b) (which can be written as f ∈ C1 (a, b)) if the following two conditions are true:
- The function is differentiable on (a, b),
- f′: (a, b) → ℝ is continuous.
Where:
- f = a function
- f′ = derivative of a function (′ is prime notation, which denotes a derivative).
- ℝ = the set of all real numbers (“reals”).
- ∈: “Is an element of”.
- (a, b): an interval from a to b.
Example
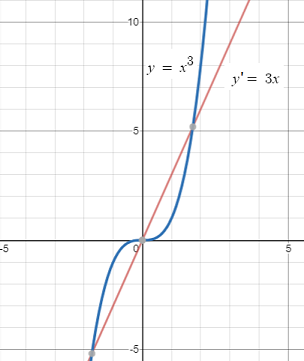
The function f(x) = x3 is a continuously differentiable function because it meets the above two requirements.
- The derivative exists: f′(x) = 3x
- The function is continuously differentiable (i.e. the derivative itself is continuous)
See also: Continuous Derivatives.
Do All Differentiable Functions Have Continuous Derivatives?
When you first studying calculus, the focus is on functions that either have derivatives, or don’t have derivatives. You may be misled into thinking that if you can find a derivative then the derivative exists for all points on that function. However, a differentiable function and a continuous derivative do not necessarily go hand in hand: it’s possible to have a continuous function with a non-continuous derivative.
One example is the function f(x) = x2 sin(1/x). Despite this being a continuous function for where we can find the derivative, the oscillations make the derivative function discontinuous. You can find an example, using the Desmos calculator (from Norden 2015) here.
Infinitely Differentiable Function
An infinitely differentiable function can be differentiated an uncountable, never ending, number of times. More precisely, if a function f has derivatives f (n): (a, b) → ℝ of all orders n ∈ N, then f is infinitely differentiable on the open interval (a, b) [1]. “All orders” means first derivative, second deritive, and so on, ad infinitum.
Infinitely differentiable function examples: All polynomial functions, exponential functions, cosine and sine functions. Any combination, product, or sum of these functions. A specific example is the polynomial function f(x) = xy. Note that at some point, the derivative will equal zero, but that doesn’t mean it isn’t differentiable: the derivative of 0 is just 0 again, and so on.
Complex functions are infinitely differentiable if they are differentiable once; In other words, if you can find the first derivative of a complex function, then you can find them all.
On the other hand, an example of a non-infinitely differentiable function is the absolute value function f(x) = |x|; The derivative does not exist at x = 0.
Infinitely Differentiable Function vs. Smooth Function
Sometimes, infinitely differentiable functions are sometimes called smooth functions (and vice versa), but there is a subtle difference: smooth functions do not have to be infinitely differentiable (although they often are). Generally speaking, smooth functions have continuous derivatives up to a certain order, say the 10th derivative. If a smooth function has derivatives of all orders, up to infinity, then those smooth functions are also infinitely differentiable.
Similarly, an analytic function is an infinitely differentiable function; Infinitely differentiable functions are also often analytic for all x, but they don’t have to be [2, 3]. A function defined on a closed interval is analytic, if for every point x0, there is a corresponding Taylor series with a positive radius of convergence that converges to f(x) in in the neighborhood of x0. A Taylor series has a derivative of a Taylor series with the same radius of convergence, and it converges uniformly in every closed interval containing x0; This means that an analytic function is also infinitely differentiable on the specified interval [4].
How to Figure Out When a Function is Not Differentiable
In general, a function is not differentiable for four reasons:
You’ll be able to see these different types of scenarios by graphing the function on a graphing calculator; the only other way to “see” these events is algebraically. Even if your algebra skills are very strong, it’s much easier and faster just to graph the function and look at the behavior.
How to Check for When a Function is Not Differentiable
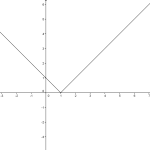
Step 1: Check to see if the function has a distinct corner. For example, the graph of f(x) = |x – 1| has a corner at x = 1, and is therefore not differentiable at that point:
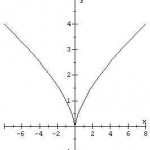
Step 2: Look for a cusp in the graph. A cusp is slightly different from a corner. You can think of it as a type of curved corner. This graph has a cusp at x = 0 (the origin):
Step 3: Look for a jump discontinuity. This normally happens in step or piecewise functions. The function may appear to not be continuous. The following graph jumps at the origin.
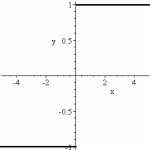
Step 4: Check for a vertical tangent. A vertical tangent is a line that runs straight up, parallel to the y-axis.
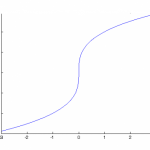
This graph has a vertical tangent in the center of the graph at x = 0.
Limits and Differentiation
Technically speaking, if there’s no limit to the slope of the secant line (in other words, if the limit does not exist at that point), then the derivative will not exist at that point. The “limit” is basically a number that represents the slope at a point, coming from any direction.
Nowhere Differentiable
A nowhere differentiable function is, perhaps unsurprisingly, not differentiable anywhere on its domain. These functions behave pathologically, much like an oscillating discontinuity where they bounce from point to point without ever settling down enough to calculate a slope at any point.
Example of a Nowhere Differentiable Function
Many of these functions exists, but the Weierstrass function is probably the most famous example, as well as being the first that was formulated (in 1872). Named after its creator, Weierstrass, the function (actually a family of functions) came as a total surprise because prior to its formulation, a nowhere differentiable function was thought to be impossible.
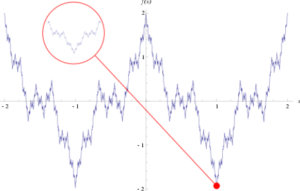
Many other classic examples exist, including the blancmange function, van der Waerden–Takagi function (introduced by Teiji Takagi in 1903) and Kiesswetter’s function (1966).
The following very simple example of another nowhere differentiable function was constructed by John McCarthy in 1953:
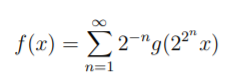
Where: where g(x) = 1 + x for −2 ≤ x ≤ 0, g(x) = 1 − x for 0 ≤ x ≤ 2 and g(x) has period 4.
References
[1] Chapter 4: Differentiable Functions.
[2] Zhang, F. (2016). Analytic Functions …. Retrieved October 27, 2021 from: https://blogs.ubc.ca/2015math100/2016/03/17/analytic-functions-and-infinitely-differentiable-functions/
[3] Notes on Analytic Functions.
[4] Analytic Functions And Classes Of… Functions: Rice Institute Pamphlet, V29, No. 1, January, 1942
Chapter 4. Diff. Functions. Retrieved November 2, 2019 from: https://www.math.ucdavis.edu/~hunter/m125a/intro_analysis_ch4.pdf
Karl Kiesswetter, Ein einfaches Beispiel f¨ur eine Funktion, welche ¨uberall stetig und nicht differenzierbar ist, Math.-Phys. Semesterber. 13 (1966), 216–221 (German)
Larson & Edwards. Calculus.
McCarthy, J. An everywhere continuous nowhere diff. function. American Mathematical Monthly. Vol. LX, No. 10, December 1953.
Norden, J. Continuous Differentiability. Retrieved November 2, 2015 from: https://www.desmos.com/calculator/jglwllecwh
Desmos Graphing Calculator (images).
Rudin, W. (1976). Principles of Mathematical Analysis (International Series in Pure and Applied Mathematics) 3rd Edition. McGraw-Hill Education.
Su, Francis E., et al. “Continuous but Nowhere Differentiable.” Math Fun Facts.
T. Takagi, A simple example of the continuous function without derivative, Proc. Phys.-Math. Soc. Tokyo Ser. II 1 (1903), 176–177.