A displacement function tells us how far a particle has moved from a starting point (an origin) at an given time.
Note that displacement is not the same as distance traveled; while a particle might travel back and forth or in circles, the displacement only represents the difference between the starting and ending position. It is a vector quantity, which means it has both a value and a direction (e.g. 20 m north or minus 50 feet). It is only equal to the distance traveled if the motion is straight line in a constant direction.
Finding the Displacement Function in (Relatively) Simple Situations
Example question: Suppose a ball is traveling with an initial velocity of 11 m/s and a acceleration of 2 m/s down a slope. What is the displacement at t = 2?
The formula to find the displacement (Δ s) is:
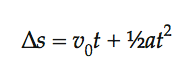
Step 1: Identify the parts of the equation (from the question):
- v0 = 11 m/s
- t = 2 s
- a = 2 m/s
Step 2: Insert the values into the formula and solve.
By the above equation, the displacement at t = 2 will be:
( 11 m/s · 2 s) + (½ · 2 m/s · 2 s2),
Giving the answer as 22 m + 4 m = 26 m.
How is the Formula Derived?
Let’s say a two-dimensional particle is undergoing motion in some constant direction (imagine a dot on a number line).
The speed of the particle can be changing, but to make the math easy, let’s say that the acceleration is constant.
Acceleration is defined as the change in velocity per unit time, so if you have a starting velocity and a constant acceleration, you can write the acceleration at any given time in terms of the velocity:
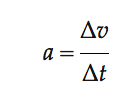
or
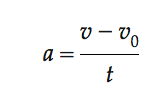
Using a little algebra, you can write the velocity in terms of the acceleration:
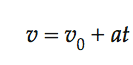
Velocity is the change in position per unit time, so the velocity of a particle is the first derivative of the position.
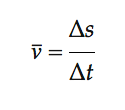
and
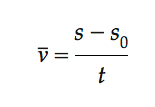
With a little rearrangement and algebraic substitution, you get:
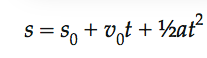
Setting the initial distance to 0, you get an equation which gives you the displacement, or change in position.
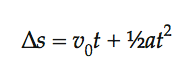
References
Distance, Displacement and Position. Retrieved from https://washingtonlee.apsva.us/wp-content/uploads/sites/38/2017/02/Distance-Displacement-and-Position-Notes.pdf on Feb 26, 2019
Elert, Glenn. Equations of Motion. The Physics Hypertext. Retrieved from https://physics.info/motion-equations/ on Feb 27, 2019.