Parametric Function / Equation: Definition, Examples

Contents:

What are Parametric Functions?
Parametric Derivatives

What are Parametric Functions?

A parametric function is really just a different way of writing functions, just like explicit and implicit forms:

Explicit functions are in the form y = f(x), for a < x < b. These include:
- Rational functions (e.g., f(x) = (x² − 1) / (x + 19)),
- Exponential functions (e.g., f(x) = 2^x)
- Polynomial functions (e.g., f(x) = x² 5 + 12).
Implicit functions, which describe shapes like circles, hyperbolas and parabolas. They take the form: f(x, y) = 0 for a < x < b and c < y < d.
The parametric function takes the form: p(t) = (f(t), g(t)) for a < t < b.

More specifically, a parametric function expresses certain quantities in terms of one or more independent variables called “parameters.” Multiple dependent variables x and y are treated as a single entity, which depend on an explicit independent variable (e.g. t). The range of a parameter function is a set of ordered pairs (x, y).

Formula

A parametric function is any function that follows this formula:
p(t) = (f(t), g(t))
for a < t < b.

Varying the time(t) gives differing values of coordinates (x,y).

In the above formula, f(t) and g(t) refer to x and y, respectively. Some authors choose to use x(t) and y(t), but this can cause confusion. That’s because if you use x(t) to describe the function value at t, x can also describe the input on the horizontal axis.

Example

The implicit form for a circle is: x² + y² = r². The parametric equation for a circle is:
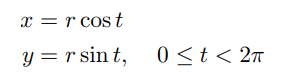
parametric function

Parameterization and Implicitization

Suppose we want to rewrite the equation for a parabola, y = x², as a parabolic function. The easiest way to do this is to introduce a new, free parameter—we can call it t. Then we can say:

We’ve just parameterized our function.

Implicitization is the opposite of parameterization. It means taking a parametric function and changing it back into a single formula with an implicit relationship between x and y.

For the parabola, it’s super simple: since x = t, replace t² with x² and you are back to your implicit formula.

Let’s look at something just a little more complicated. The parametric formula for a circle of radius a is

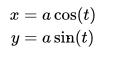
We can divide both sides by a, and so rewrite this as

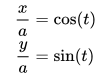
The Pythagorean Triangle Identity gives us

Substituting our parametric functions into that, we get

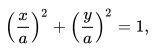
And so, finally

Which is the (standard) implicit equation for a circle a; so we’ve successfully implicitized it.

Use of Parametric Functions

In introductory calculus classes, parametric functions are usually taught as being representations of graphs of curves, but they can be used to model a much wider variety of situations. For example:

They are useful for Modeling the paths of moving objects,
They are necessary for optimizing multivariable functions.
In general, they enable complicated problems with multiple inputs to be reduced to a simpler function (Stalvey, (2014).

Parametric to Rectangular Forms

What are Rectangular Form and Parametric Form?

Rectangular form (also called Cartesian form) refers to rectangular coordinates— the familiar (x, y) coordinates. A function written in rectangular form is y = f(x).

Parametric form is just a different way of writing the same equation. For example, the equation y = x², which is in rectangular form, can be rewritten as a pair of equations in parametric form: x = t and y = t². Conversion to parametric form is called parameterization.

Parametric to Rectangular Forms

The general steps for converting from parametric to rectangular forms are:

Solve one equation for t or x,
Plug the solution into the other equation,
Tidy up your answer.

Which variable you solve for depends on the format of the equations you’re given. Look for the variable that appears on the right-hand side of both equations. This first example shows you one problem where solving for “t” is the best approach; the second example shows you solving for x.

Example #1 :Convert the following from parametric to rectangular form:
x = t + 1, y = t – 2.

Step 1: Solve one of the equations for t. It doesn’t matter which you choose, but for this example I’ll solve x = t + 1 for t:

x = t + 1
Switch sides: t + 1 = x
Subtract 1 from both sides: t + 1 (-1) = x (-1)
Simplify: t = x – 1

Step 2: Replace t in the second equation (the one you didn’t choose in Step 1) with the result you obtained in Step 1:

y = t – 2
Substitute t for the Step 1 result: y = (x – 1) – 2
Simplify: y = x – 3

Example #2:Convert the following from parametric to rectangular form:
y = 4x + 5, t = x + 1

Step 1: Solve one of the equations for x. For this example I’ll solve t = x + 1 for t:

t = x + 1
Switch sides: x + 1 = t
Subtract 1 from both sides: x + 1 (-1) = t (-1)
Simplify: x = t – 1

Step 2: Replace x in the second equation (the one you didn’t choose in Step 1) with the result you obtained in Step 1:

y = 4x + 5
Substitute x for the Step 1 result: y = 4(t – 1) + 5
Simplify:
- y = 4t – 4 + 5
- y = 4t + 1

Parametric to Rectangular Forms: References

Pilkington, A. Curves Defined by Parametric Equations. Retrieved July 11, 2021 from: https://www3.nd.edu/~apilking/Math10560/Lectures/Lecture%2034.pdf

Parametric Derivatives

What is a Parametric Derivative?

If φ = (x(u), y(u)) is the parametric equation for a curve, the parametric derivative of the curve at a point ₀ is the vector:
Φ′ (₀) = [′ (₀), ′ (₀)]

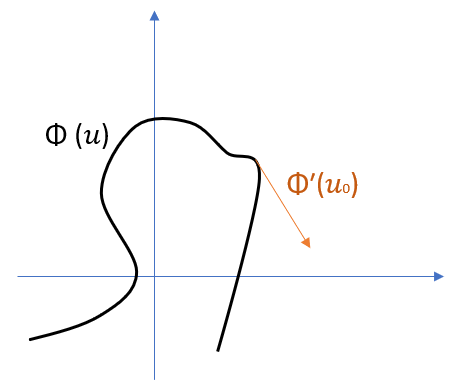
The parametric derivative is a tangent line, with length. The vector’s direction, which points tangent to the curve, depends on the path of the curve. Its magnitude is determined by the tracing speed [1].

How to I Find a Parametric Derivative?

The formula to find a parametric first derivative is:

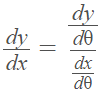
I used θ here as an example, but you may also differentiate with respect to t or another variable.

Example Question: Find the parametric derivative of the curve defined by x = cos(θ), y = 2sin(θ) when θ = (5π)/6.

Step 1: Calculate the derivative for both functions:

x = cos(θ): dx/dθ = -sin (θ)
y = 2sin(θ): dy/dθ = 2cos (θ)

Step 2: Plug the derivatives from Step 1 into the formula, along with the given value:

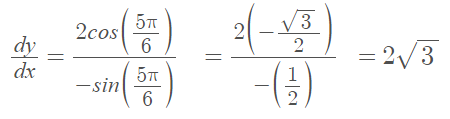
That’s it!

The second derivative formula is a little different from the “usual” second derivative. You can’t just take the derivative of the first derivative. Instead, take the derivative of the first derivative divided by the derivative of the original x term [2]:

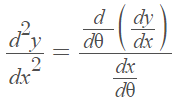
Parametric Derivative: References

Graph: Desmos.com
[1] Kazhdan, M. Parametric Curves. Retrieved July 8, 2021 from: http://www.cs.jhu.edu/~misha/Fall20/20.pdf
[2] Math 231E, Lecture 33. Parametric Calculus. Retrieved July 8, 2021 from: https://faculty.math.illinois.edu/~rdeville/teaching/231-16/lectures/Lecture33.pdf

Other References

McQuarrie, B. Precalculus: Parametric Representations. Retrieved May 20, 2019 from: http://cda.mrs.umn.edu/~mcquarrb/teachingarchive/Precalculus/Lectures/ParametricRepresentations.pdf
Stalvey, H. (2014). The Teaching and Learning of Parametric Functions: A Baseline Study. Retrieved May 20, 2019 from: https://scholarworks.gsu.edu/math_diss/18/
Wilson, M. Assignment Ten: Investigating Parametric Functions. Retrieved May 20, 2019 from: http://jwilson.coe.uga.edu/EMAT6680Fa11/Wilson/MGW_10/mgw_10.html