Constant Function: Definition, Graph, & Examples

Types of Functions >

Contents:

1. What is a Constant Function?
2. Graph of a Constant Function
3. Derivative of a Constant
   • Constant Factor Rule
   • Constant multiplied by a power function
4. Integral of a Constant Function
5. Limit of a Constant Function
6. Applications of a Constant Function

What is a Constant Function?

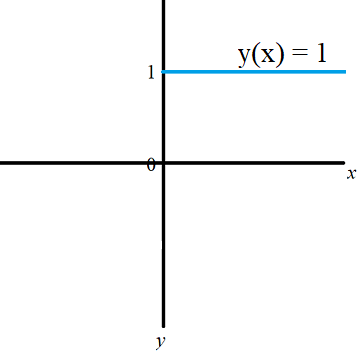
A constant function is where the output variable (y) is not dependent on the input variable (x). Generally, it is a function that always has the same value no matter what the input is. For example:

• If x = 0, y = 1
• If x = 1, y = 1
• If x = 2, y = 1

We can write this type of function as:

f(x) = c

Where:

• c is a constant: a number that doesn’t change as x changes.

Examples of constant functions:

• f(x) = 99,
• f(x) = .1 and
• f(x)= -21

Since f(x) is equal to a constant, the value of f(x) will always be the same no matter what the value of x might be.

Back to Top.

The Graph of a Constant Function

In a two dimensional plane, the graph of this type of function is a straight, horizontal line. It passes through the point (0, c), (1, c), and (-1, c), where c is the same number and a is any number on the number line.

For example, the graph of the constant function f(x) = 4 is a straight, horizontal line that passes through the points (2,4), (0,4), and (-2,4). This graph is shown below.

Back to Top.

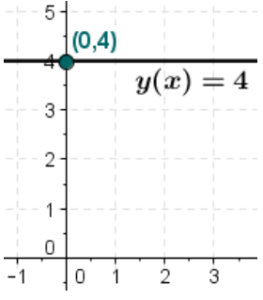
1. Derivative of a Constant

While most of the rules require you to complete several steps, taking the derivative of a constant only requires you to perform one step:

Change the constant to a 0, because the derivative or slope of any constant function is equal to zero.

In other words, if f(x) = c, then f′(x) = 0.

As a formula, that’s:

The rule is sometimes called the constant rule.

The “rule” is really a shortcut; using it allows you to bypass having to take the limit to find the derivative of any constant function.

Examples

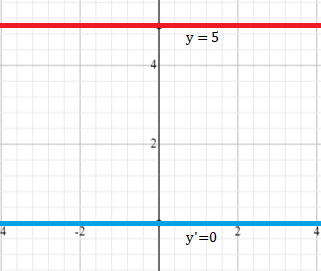
Derivative of a Constant:

• If f(x) = 5, then f&prime(x) = 0,
• If f(x) = -2, then f′(x) = 0,
• If f(x) = 10000000, then f′(x) = 0,
• If f(x) = 55 1/3, then f′(x) = 0,
• If f(x) = √9, then f′(x) = 0,

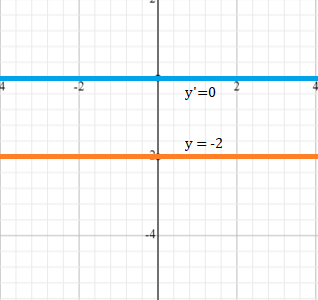
That’s it!

Tip: You can use direct substitution to arrive at the same answer (i.e. that the derivative is zero).

Note About Similar Functions

The rule that the derivative of a constant only applies if you take the derivative of a constant (aka a polynomial function of zeroth degree), and not constants that also have exponents, constants multiplied by x, or anything other than a number. While √9 is a constant, √9x is not. If in doubt, graph your function. If the result is a horizontal line, then your function is a constant.

Back to Top.

2. Constant Factor Rule

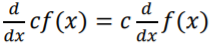
The constant factor rule is a way to find the derivative for a function that has a constant factor. You’re probably more used to constant factors being called “coefficients.” so the rule could just as well be called the coefficient rule.

What is a Constant Factor?

A Constant factor (also called a numerical coefficient or just coefficient) is just a number (a constant) that appears in front of a function. It’s just a value that doesn’t depend on x (or any other inputs).

Constant factors are quite common with trigonometric functions and polynomial functions. For example:

• f(x) = 3 sin x has a constant factor of 3,
• f(x) = -6x² has a constant factor of -6.

How to Use the Constant Factor Rule

Essentially, you just ignore the constant factor: pull it out in front and forget about it. You only need to find the derivative of the portion that’s not a constant.

Example, find the first derivative of f(x) = 3 sin(x)

• Write the derivative notation: f^′ = 3 sinx(x)
• Pull the constant out in front: 3 f^′ = sinx(x)
• Find the derivative of the function (ignoring the constant):
  3 f^′ = cos(x)
• Place the constant back in to where it was in the first place:
  = 3 cos(x)

Formal Definition of the Constant Factor Rule

The formal definition of the rule is as follows (Simonds & Jordan, 2020):

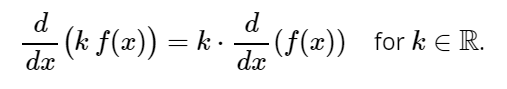
Where:

• k = a constant,
• ℝ = the set of real numbers.

Back to Top.

3. Constant multiplied by a power function

The derivative of a constant is always zero and the derivative of a function depends upon what kind of function it is (for example, you can differentiate exponents with the power rule). Intuitively, you might think that a constant multiplied by a function is zero, because the derivative of a constant is zero (0 * anything = 0). However, differentiation in calculus isn’t always intuitive; the derivative of a constant multiplied by a power rule function is actually equal to the constant times the derivative of the function.

Example Question 1: What is the derivative of 5x³?

Step 1: Separate the constant from the function.
5
x³

Step 2: Differentiate the function using the rules of differentiation. The function x³ is an exponent and so is differentiated using the power rule:
d/dx [x³] = 3x^{3 – 1} = 3x²

Step 3: Place the constant back in front of the derivative of the function from Step 2:
5(3^x2)

Step 4: Use algebra to multiply through:
5(3^x2) = 15x²

Example Question 2: What is the derivative of -7x^-4?

Step 1: Separate the constant from the function.
-7
x^-4

Step 2: Differentiate the function using the rules of differentiation. The function x^-4 is an exponent and so is differentiated using the power rule:
d/dx [x^-4] = -4x^-4-1 = -4x^-5

Step 3: Place the constant back in front of the derivative of the function from Step 2:
-7[-4x^-5]

Step 4: Use algebra to multiply through:
-7[-4x^-5] = 28x^-5 = 28/x⁵

That’s it!

Back to Top.

Integral of a Constant Function

The integral of this type of function is equal to c x. For example, the integral of f(x) = 10 is 10x.

The following shows the graph of f(x) = 10, and the integral f(x) = 10x. The blue square represents the integral when evaluated from 0 to 1.

Back to Top.

Limit of a Constant Function

The limit of a constant function (according to the Properties of Limits) is equal to the constant. For example, if the function is y = 5, then the limit is 5.

Applications of the Constant Function

Though it is one of the simplest type of functions, it can be used to model situations where a certain parameter is constant and isn’t dependent on the independent parameter. For example, a school dining room where every child was given one donut, irrespective of age, or an exam in which every student was given a C regardless of how hard they worked.

References

Images created partly with the Symbolab graphing calculator.
Larson, R. & Edwards, B. (2008). Calculus of a Single Variable. Cengage Learning.
Migliore, E. (2005). Review of Basic Algebra Concepts.
Simonds, S. Jordan, A. (2020). 5.4The Constant Factor Rule. Calculus Lab Manual MTH 251 at Portland Community College. Retrieved July 27, 2020 from: http://spot.pcc.edu/math/clm/section-constant-factor-rule.html
Maplesoft Support. Online Help: Math Apps: Functions and Relations. Retrieved from https://www.maplesoft.com/support/help/Maple/view.aspx?path=MathApps%2FConstantFunction on May 24, 2019.