What is a Definite Integral?
Watch the video or read on below:
Definite integrals give a result (a number that represents the area) as opposed to indefinite integrals, which are represented by formulas.
While Riemann sums can give you an exact area if you use enough intervals, definite integrals give you the exact answer—and in a fraction of the time it would take you to calculate the area using Riemann sums (you can think of a definite integral as being an infinite amount of intervals in a Riemann sum). The definite integral is also known as a Riemann integral (because you would get the same result by using Riemann sums).
Formal definition for the definite integral:
Let f be a function which is continuous on the closed interval [a,b]. The definite integral of f from a to b is the limit:
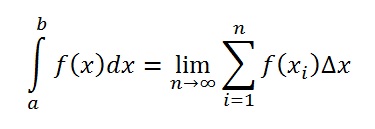
Where:
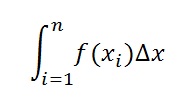
is a Riemann sum of f on [a,b].
The formal definition of a definite integral looks pretty scary, but all you need to do is to calculate the area between the function and the x-axis. You’ll need to understand how to apply the rules for indefinite integrals in order to calculate a definite integral.
How to Find a Definite Integral
Special case: If the equation you’re dealing with contains both a function and that function’s derivative, then you’ll probably want to use u-substitution instead of following the steps below. For example:
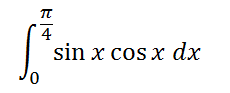
Example problem:
Example problem #1: Calculate the area between x = 0 and x = 1 for f(x) = x2.
Step 1: Set up integral notation, placing the smaller number at the bottom and the larger number at the top:
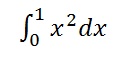
Step 2: Find the integral, using the usual rules of integration. Here, you’ll apply the power rule for integrals, which is:
Note though, that as you’re finding a definite integral (as opposed to an indefinite one), you won’t be needed that “+ c” at the end. Applying that rule gives:
∫ xndx = x2 + 1⁄(2 + 1)
= x3 / 3
Writing that a little more neatly, with the limits of integration (0, 1) included:
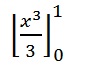
Step 3: Substitute the top number for x and then solve:
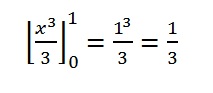
Step 4: Add a subtraction sign and then substitute the bottom number for x, solving the integral:
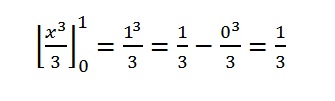
That’s it!
Tip: There in another kind of definite integral, called a contour integral. Contour integrals involve those definite integrals that are taken on the complex plane (as opposed to the real line). However, you’re unlikely to encounter contour integrals in elementary calculus classes.