The regularized incomplete beta function (also called the regularized beta function) is widely used in statistics and some areas of physics as the cumulative distribution function of the beta distribution [1]. It represent the CDF for a random number Y that obeys the beta distribution [2].
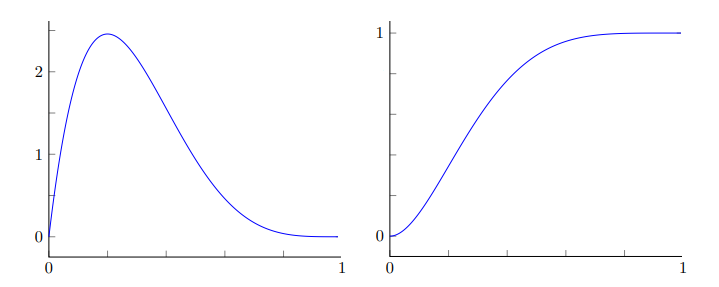
The regularized incomplete beta function is used when it’s inconvenient to calculate the incomplete beta function on its own. The “regularized” version divides this function by the complete beta function [4], hence another alternate name — the incomplete beta function ratio [5].
Formula for the Regularized Incomplete Beta Function
The regularized incomplete beta function is defined in terms of the incomplete beta function B(z; a, b) — also called the Euler integral — and the complete beta function b (a. b) [6]:
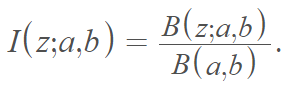
The basic definition shown above cannot be used for nonpositive integers a or b, as this will lead to an indeterminate expression. For nonpositive integers, you may need to use a more complete definition such as [7]:
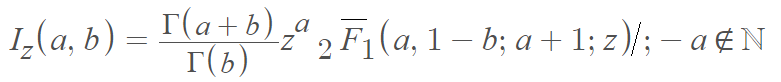
References
[1] Conte, E. On a Simple Derivation of the Effect of Repeated Measurements on Quantum Unstable Systems by Using the Regularized Incomplete Beta Function. Adv. Studies Theor. Phys., Vol. 6, 2012, no. 25, 1207 – 1213.
Retrieved June 18, 2022 from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.856.387&rep=rep1&type=pdf
[2] Nordén, B. et al. (Eds.). (2020). Entropy-Enthalpy Compensation. Finding a
Methodological Common Denominator Through Probability, Statistics, and Physics. Jenny Stanford Publishing.
[3] Ireland, F. (2018). GPU accelerated risk quantification. Master’s Thesis.
[4] Wolfram, S. (2003). The Mathematica Book Volume 1. Wolfram Media.
[5] Muller-Bungart, M. (2007). Revenue Management with Flexible Products. Models and Methods for the Broadcasting Industry. Springer.
[6] Weisstein, E. (1999). Regularized Beta Function. Retrieved June 18, 2022 from: https://archive.lib.msu.edu/crcmath/math/math/r/r199.htm
[7] Wolfram. BetaRegularized. Retrieved June 18, 2022 from: https://functions.wolfram.com/GammaBetaErf/BetaRegularized/02/01/