Relation vs Function

Calculus Problem Solving >

A relation is a set of ordered pairs. It is a way of showing how two sets are related to each other. A function is a special type of relation where each input has a single output.

Relation vs Function Explained

A relation is any set of ordered pairs. It is a way of showing how two sets are related to each other. For example, {(1, 2), (6, 9), (8, 11)} or {(22, 2), (22, 9), (101, 11)}. Relations are often used to model real-world phenomena. For example, the relation {(student, teacher)} can be used to model the relationship between students and teachers in a school.

A function is a specific type of relation where no two pairs have the same first coordinate. To put that another way, the first element in the pair (the domain) is mapped to exactly one of the second elements (the range). For example:

• {(1, 2), (6, 9), (8, 11)} is a function,
• {(22, 2), (22, 9), (101, 11)} is not a function (22 maps to two elements, not one).

Functions are often used to model mathematical concepts. For example, the function f(x) = x² can be used to model the area of a square with side length x.

All functions are relations, but the converse is not true: not all relations are functions. For example, consider the relation {(1, 2), (2, 3), (3, 4), (4, 1)}. This relation has two outputs for the input 1, namely 2 and 4. Therefore, it is not a function.

How do I tell if it’s a relation or a function?

Graphically, you can spot a function by using the vertical line test. The basic idea is to draw a few vertical lines spread out on the graph. If each line crosses the graph only once, it is a function. If not, then it’s not a function. Note that the vertical line test can’t tell you if you have a relation or a function though, because by definition all functions are relations.

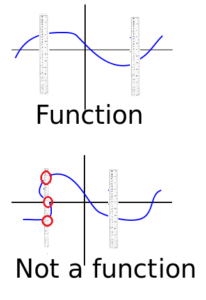
The graph of the relation {(x, y) | x and y are siblings} does not pass the vertical line test (so is not a function). This is because the vertical line can intersect the graph in more than one point, depending on the values of x and y.

Some other ways to spot a relation graphically:

• If the graph has multiple y-values for a single x-value, then it is not a function.
• If the graph has a hole or gap, then it is not a function.
• If the graph has a cusp or a sharp turn, then it is not a function.

Example of Relation vs Function

The relation (son, father) is a function because the first element in the pair (son) maps to one father. The relation (father, son) isn’t a function because it’s possible for a father to have more than one son.

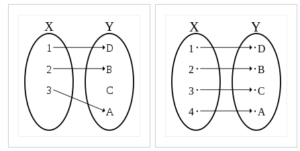
Relation vs Function: Notes from Set Theory

In set theory, the terms function and relation are defined a little differently. In the terms single-valued function or multiple-valued function, the word “function” means a relation. It doesn’t mean “function” in the calculus sense of the word. Set theory also has several different types of relation, such as (MacNeil, 2013):

• Transitive relation: Implies that a leads to b leads to c. For example, all Londoners are English and all English are British, which implies that all Londoners are British.
• Symmetric relation: Ato B implies B to A. For example, marriage between two people is symmetric.
• Reflexive relation: Applies to members of one set only. For example, a certain quantity might weigh 1 oz or 28.3495. They are the same weight in different units.

References

Grigorieva , E. (2015). Methods of Solving Nonstandard Problems. Springer International Publishing.
MacNeil, D. (2013). Fundamentals of Modern Mathematics: A Practical Review. Dover Publications.