Contents (Click to skip to that section):
Dirac’s Delta Function?
Dirac’s Delta function (also called the delta function, impulse function, or unit-impulse function) isn’t actually a “function” in the strict definition of the word. Many “generalized functions” (or rather, non-functions) like this describe real-world phenomena that can’t adequately be described by functions in the usual sense. In the case of Dirac’s delta, it models a unit impulse, passing through a system in an infinitely short period of time.
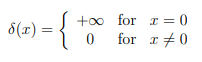
Named after the nuclear physicist Paul Dirac, this function is mainly used in classical and quantum mechanics.
Formula for Dirac’s Delta Function
The formula is:
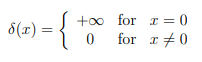
The unusual aspect about this generalized function is that it’s zero everywhere except for one instant in time, at x = 0.
Usefulness of Dirac’s Delta Function
If the function is zero everywhere, except for one instant (at x = 0), it might seem that the function doesn’t have any real world uses. However, the opposite is true: many physical processes take place instantaneously. Richards & Youn (1995) offer the following example:
“Think…of an object being struck by a hammer…the whole thing takes place: Bang!—in an instant.”
The fact that the process took place in an instant doesn’t mean that nothing interesting happened. To the contrary, a compression took place which hammered the nail into an object. These instantaneous events are commonplace in physics, especially when dealing with the sub-atomic world and in signal processing. In calculus, the function plays an important role in dealing with differential equations.
Is there a graph of Dirac’s Delta Function?
No. Dirac’s delta function can’t be graphed. That’s because the function is zero for all values of x, except where x = 0, where it equals infinity .
The Dirac function can be represented in other visual ways. For example, as a fully transparent dot on an opaque background; the area of the dot is proportional to the function’s mass (Ebbeni, 1987).
Derivatives and the Dirac function
The Dirac function is the derivative of the Heaviside function. If you take the derivative of the Dirac function, the result is the unit-moment function.
What are Generalized Functions?
Generalized functions (also called distributions) are a fairly new concept in mathematics. They are not a “type” of function, but rather a completely new way of defining them. Unlike the “usual” type of function, they have no values. Instead, they take carefully defined “test” functions and return real numbers.
The new definition is written as:
f is a rule, that given a test function φ(x) returns a number f {φ)2
A “test” function is just a sufficiently good one. (See below for the requirements for φ)
Their usefulness is in expressing formerly inexpressible phenomena, like the happenings of a physical process at an exact time(t). Formerly, an instantaneous event could only be measured by averaging the values around that point (for example, by finding a limit). With this new function definition, it’s possible to find derivatives and integrals for the strangest of function behaviors.
Why do We Need a New Definition??
The the usual idea of a function—a mapping of one set of objects to another— isn’t adequate for describing all natural phenomenon.
As an example, let’s say you wanted to create a function that represented the force of the impact of the meteor that wiped out the dinosaurs. The only value in that function would be at the exact moment the meteor hit the Earth. We can call that t = 0. At t = 0, the function has a value approximately equivalent to 10 billion atomic bombs. The impact would have been over in a flash. Every other value for “t” would equal zero. Up until the introduction of generalized functions, it wasn’t possible to use functions to describe this process, or any others like it.
This problem with recognizing that many, many physical processes are impossible to represent by the usual idea of a function is why the concept of a generalized function was developed.
As an idea, generalized functions are fairly abstract. For example, while a function has a definite value at a point, this is not true of generalized functions; they technically do not have any values other than in one tiny point. The fact that the generalized function doesn’t have any definite values at any point may lead you to wonder why they exist in the first place. The problem isn’t that they don’t exist (they do, and have a wide variety of applications, especially in physics).
Requirements for φ
φ is at the center of the new definition for a generalized function; it has some very specific requirements.
- φ is (perhaps surprisingly) a real function that maps from ℝ → ℝ in some set. (Note: ℝ is notation for “the set of all reals)
- φ is infinitely differentiable.
- φ is allowed to be nonzero only in a specified, finite region.
- φ is a smooth function with a noticeable “bump.”
- φ must be linear (i.e. it must act like integration).
- For every continuous change of φ(x), there must be a corresponding continuous change in f{φ}.
References
Beckenbach, E. (2013). Modern Mathematics for the Engineer: Second Series. Courier Corporation.
Ebbeni, J. (1987). Progress in Holography: 31 March-2 April 1987, The Hague, The Netherlands, Volume 812. SPIE–The International Society for Optical Engineering.
Johnson, S. (2017). When functions have no value(s):
Delta functions and distributions. Retrieved December 6, 2019 from: https://math.mit.edu/~stevenj/18.303/delta-notes.pdf
Oldham, K. et al. (2010). An Atlas of Functions: with Equator, the Atlas Function Calculator. Springer Science & Business Media.
Richards, J. & Youn, H. (1995). The Theory of Distributions: A Nontechnical Introduction. CUP Archive.