Contents:
Convex Function Definition
A convex function has a very distinct ‘smiley face’ appearance. A line drawn between any two points on the interval will never dip below the graph.
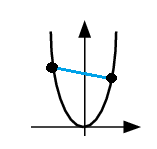
It’s more precisely defined as a function where, for every interval on its domain, the midpoint isn’t larger than (higher than) the arithmetic mean of the values (heights) at the ends of the interval.
A few examples of convex functions:
- eax
- − log(x)
- x|a|, a ≥1
Graphical Examples of Convex and Non Convex Functions
The easiest way to figure out if a graph is convex or not is by attempting to draw lines connecting random intervals.
On the left is a convex curve; the green lines, no matter where we draw them, will always be above the curve or lie on it.
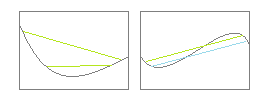
On the right, we are able to draw a number of lines between points on the graph which actually do dip below the graph. (Two are shown, drawn in green and blue). This curve is not convex at all on the interval being graphed.
Mathematical Definition of a Convex Function
The use of Greek letters makes the technical definition of a convex function look as if it was something complicated; but in fact, all it says is what was stated above: for any two points, the average of their value must be larger than the values of their midpoints.
We write that this way:
a function f(x) is convex on an interval [a,b] if for any two points x, y on the interval, and 0 ≤ λ ≤ 1
![]()
Closed Function
In convex analysis, a closed function is a convex function with an epigraph that is a closed set.
The epigraph is the set of points laying on or above the function’s graph. A convex function has an epigraph that is a convex set. If you’re unfamiliar with epigraphs and convex sets, this image shows you the basic idea behind those terms (Duchi, 2016):
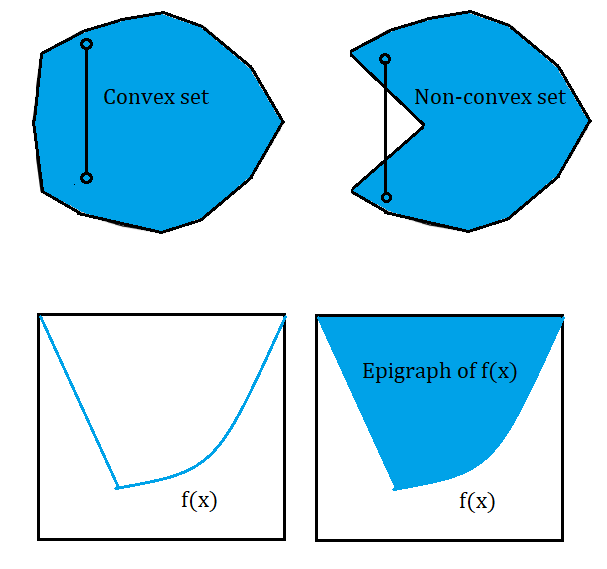
Perhaps not surprisingly (based on the above images), any continuous convex function is also a closed function.
While the concept of a closed functions can technically be applied to both convex and concave functions, it is usually applied just to convex functions. Therefore, they are also called closed convex functions. For concave functions, the hypograph (the set of points lying on or below its graph) is a closed set.
Closed Function Examples
As well as convex functions, continuous on a closed domain, there are many other functions that have closed set epigraphs. For example, all differentiable convex functions with Domain f = Rn are also closed.
The following general families of functions are all closed:
- Affine functions [f(x) = a′x + b],
- Continuous functions,
- Norms.
- Quadratic functions [f(x) = x′Px + a′x + b].
A couple of specific examples of a closed function:
- f(x) = -log (1 – x2) with domain f = {x| |x| <1}
- f(x) = x log x with domain f = ℝ+ and f(0) = 0
Jensen’s Inequality
Jensen’s inequality is a special inequality that has to do with convex sets. It says that if a particular function g is convex,
E[g(X)] ≥ g(E[X]).
Here E is the expected value, the mathematical expectation, or the average. It can be a probability weighted mean; so Jensen’s inequality also tells us that, if w1, w2…wn are weights such that
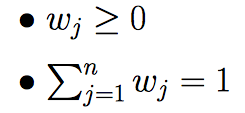
Then, for arbitrary x:
![]()
If all the xj are equal but one of the wj equal zero, then the function f(x) the ≥ sign becomes an equals sign. If this is the only time in which that inequality becomes an inequality, we say our function is strictly convex.
Applications of Jensen’s Inequality
Jensen’s Inequality is important in probability, in information theory, and in statistical physics.
In probability, it is central in the derivation of an important algorithm called the Expectation-Maximization algorithm. It also allows us to prove the consistency of maximum likelihood estimators. It can also be used to show that the arithmetic mean for a set of positive scalars is greater than or equal to their geometric mean. For how this is shown, see: Arithmetic Mean ≥ Geometric Mean.
In statistical physics, this inequality is most important if the convex function g is an exponential function, and where the expected values E are expected values with respect to a probability distribution.
In information theory, Jensen’s Inequality can be used to derive Gibbs inequality, which tells us about the mathematical entropy of discrete probability distributions.
References
Ahmadi, A.A. ORF 523 Lecture Notes: Lecture 7. Theory of Convex Functions. Retrieved from http://www.princeton.edu/~amirali/Public/Teaching/ORF523/S16/ORF523_S16_Lec7_gh.pdf on March 2, 2019
Derpanis, Konstantinos G. J’s Inequality. Version 1.0, March 2015. Retrieved from Retrieved from http://www.cs.yorku.ca/~kosta/CompVis_Notes/jensen.pdf on July 20, 2019
Duchi, J. (2016). Convex Analysis Background. Park City Mathematics Institute.
Lecture 4: Closed Functions. Retrieved January 6, 2020 from: http://www.ifp.illinois.edu/~angelia/L4_closedfunc.pdf
Grasmair, Markus. Basic Properties of Convex Functions. https://wiki.math.ntnu.no/_media/tma4180/2016v/note2.pdf
Louditski, A. Lecture 3: Convex Functions. Retrieved January 6, 2019 from: https://ljk.imag.fr/membres/Anatoli.Iouditski/cours/convex/chapitre_3.pdf
Pishro-Nik, Hossein. Introduction to Probability. Retrieved from https://www.probabilitycourse.com/chapter6/6_2_5_jensen%27s_inequality.php on July 20, 2019.
Rockafellar, R. (1996). Convex Analysis (Princeton Landmarks in Mathematics and Physics). Princeton University.
Smith, Andrew. Convex Sets and J’s Inequality. University College Dublin. Retrieved from https://www.ucd.ie/mathstat/t4media/convex-sets-and-jensen-inequalities-mathstat.pdf on July 20, 2019.
Vandenberghe, L. (2019). Conjugate Functions.