Types of Functions > Floor Function and Ceiling Function
Contents (Click to skip to that section_:
- What is a Floor Function?
- What is a Ceiling Function?
- Floor Function and Ceiling Function Properties
What is a Floor Function?
The floor function (also called the greatest integer function) rounds down a value to the closest integer less than or equal to that value. For example:
- Floor (9.9) = 6
- Floor (-9.5) = -10
- Floor (π) = 3
The floor function is similar to the ceiling function, which rounds up. Essentially, they are the reverse of each other.
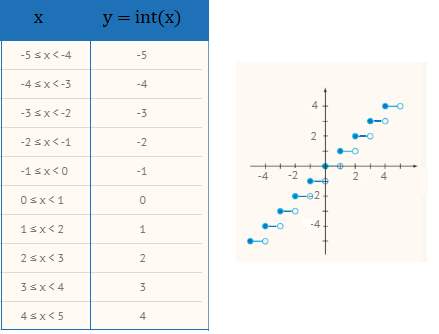
The floor function is a type of step function where the function is constant between any two integers. The table below shows values for the function from -5 to 5, along with the corresponding graph:
In computing, many languages include the floor function. For example:
- Java includes FLOOR (as well as CEIL).
- In BASIC, the floor function is called INT.
- For Mathematica, use Floor[x].
Other programming languages use the INTEGER PART function (int(x)).
You may want to use these functions to truncate numbers with many decimal places, like π.
What is a Ceiling Function?
The ceiling function (also called the least integer function) rounds up a value to the closet integer greater than or equal to that value. For example:
- Ceiling (8.9) = 9
- Ceiling (-9.5) = -9
- Ceiling (π) = 4
It’s similar to the floor function, which rounds down.
In computer science, a ceiling function takes one numerical argument and returns the smallest integer that is greater than or equal to the argument’s numeric value.
Notation for Floor Function and Ceiling Function
The name and notation for the floor function was first described by K. E. Iverson (in Graham et. al, 1990); It is usually written with square brackets missing their tops:
⌊ x ⌋.
You may also see the notation in some texts as [x], which can be confusing (is it a floor, a ceiling, or both?).
The ceiling function has similar notation, except that the “floor” part of the bracket is missing: ⌈ x ⌉. This is very similar to square brackets [ x ], but note that the missing bottom part. The floor function has similar notation, except that the “ceiling” part of the bracket is missing: ⌊ x ⌋. Sometimes, you might see other notation, including:
- Reversed boldface brackets:] x [.
- Reversed plain brackets: ] x [.
Floor Function and Ceiling Function Properties
The floor function and ceiling function ⌊ x ⌋ share a few properties.
- ⌊ x + 1 ⌋ = ⌊ x ⌋ + 1.
- ⌈ x + 1 ⌉ = ⌈ x ⌉ + 1.
- ⌈ x ⌉ = ⌊ x ⌋ if and only if x ∈ ℤ.
- ⌈ x ⌉ = ⌊ x ⌋ + 1 if and only if x ∈̷ ℤ.
- ⌊ x ⌋ = ⌈ x ⌉ + 1 if and only if x ∈̷ ℤ.
Where:
- ⌈ x ⌉ = ceiling function,
- ⌊ x ⌋ = flooor function,
- ℤ = “the set of all integers”,
- ∈ = “in the set,”
- ∈̷ = “not in the set.”
Real Life Examples
A real life example of a ceiling function can be found in postage stamps. In 2019, the cost of a first class postage stamp, up to one ounce, is 55 cents. Each additional ounce costs an extra 15 cents, up to 3 ounces. Therefore, you can say that the price(p) of a first class letter is:
p(x) = 0.55 + 0.15⌈ x – 1 ⌉, 0 < x ≤ 3.
Example: The cost of mailing a first class envelope weighing 2.8 ounces is:
p(2.8) = 0.55 + 0.15⌈ 2.8 – 1 ⌉ = 0.55 + 0.15⌈ 1.8 ⌉ = 0.55 + 0.15(2) = 0.85 (85 cents).
References
Hein, J. (2003). Discrete Mathematics. Jones & Bartlett Learning. Retrieved November 21, 2019 from: https://books.google.com/books?id=qLNfpb1hBWwC
Koshy, T. Elementary Number Theory with Applications. Retrieved November 21, 2019 from: https://books.google.com/books?id=-9pg-4Pa19IC
Koshy, T. Discrete Mathematics with Applications.