Overview of the Möbius Function
The Möbius function, μ, is a surprisingly simple sorting function that places numbers into bins. More technically, it’s an arithmetic function, widely used in number theory. One of its most important uses is in the Euler totient function.
The function μ was first described by Leonhard Euler, although it was first investigated systematically by A. Möbius (of Möbius strip fame) in 1832.
Möbius function: Definition
If you’re new to number theory, the Möbius function can be difficult to wrap your head around. The function is defined slightly differently, depending upon who is writing about it. For example, the function is defined by Zvezdelina Stankova-Frenkel (1999) as:
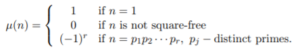
A number is “squarefree” if its prime decomposition doesn’t have any repeated factors. So, you might also see the “0” bin defined as one where a number does have one or more repeated prime factors. In addition, the superscript r is also sometimes written as a k. If the different terminologies and notations aren’t enough to get you off to a confused start, you also have to throw complex numbers into the mix.
The notation ℕ → ℂ tells you that this is an arithmetic function, mapping the set of natural numbers (whole, non-negative numbers that we use to count) to the complex plane. If you’re familiar with complex functions, that definition is probably all you need to know. But if you’re still trying to wrap your head around complex numbers, the function can be defined simply for natural numbers.
Simple Definition for Natural Numbers
The Möbius function(μ(n)) sorts natural numbers into three bins: -1, 0, and 1, based on multiples and prime factors (Pegg, 2003),
The Zero Bin
The “Zero” bin has multiples of square numbers (excluding 1):
{4, 8, 9, 12, 16, 18, 20, 24,…}.
These can be written in terms of μ:
- μ(4) = 0,
- μ(8) = 0,
- μ(9) = 0,
- μ(12) = 0,
and so on.
As you may be able to tell, the majority of numbers will fall into this bin. In fact, 6/π (about 39%) of all numbers will place into the zero bin.
Note:
Square numbers are the result of any integer multiplied by itself. For example, 2 * 2 = 4, 3 * 3 = 9. The first ten square numbers are: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100. Multiples are a product of a number and an integer. For example, the multiples of (the square number) 4 include 4 * 0 = 4, 4 * 1 = 4, 4 * 2 = 8, and so on.
The -1 Bin
This bin contains every prime number. It also contains any number that factors into an odd number of distinct primes; In other words, it’s a number where 3, 5, 7,… primes are multiplied together. For example:
- 30 (2 * 3 * 5)
- 66 (2 * 3 * 11)
- 715 (5 * 11 * 13)
- 2730 (2 * 3 * 5 * 7 * 13)
About 3/π2 numbers (about 30%) will be placed in this bin.
The +1 Bin
This bin has any number that factors into an even number of distinct primes. For example:
- 6 (2 * 3 )
- 22 (2 * 11)
- 65 (5 * 13)
- 210 (2 * 3 * 5 * 7)
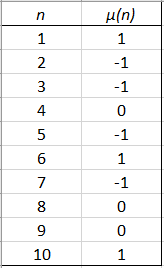
Table of Values for the Möbius Function
The first few values for the function are:
References
Abramowitz, M. and Stegun, I. A. (Eds.). “The Möbius Function.” §24.3.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 826, 1972.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford: Clarendon Press, p. 236, 1979.
Pegg, E. (2003). The Möbius Function. Retrieved December 24, 2019 from: http://www.mathpuzzle.com/MAA/02-Mobius%20Function/mathgames_11_03_03.html
Pólya, G. and Szegö, G. Problems and Theorems in Analysis, Vol. 2. New York: Springer-Verlag, 1976.
a Stankova-Frenkel, Z. (1999). Mobius Inversion Formula. Multiplicative Functions. https://math.berkeley.edu/~stankova/MathCircle/Multiplicative.pdf
Wilf, H. Generating functionology, 2nd ed. New York: Academic Press, p. 61, 1994.