Contents:
What is an Integrand?
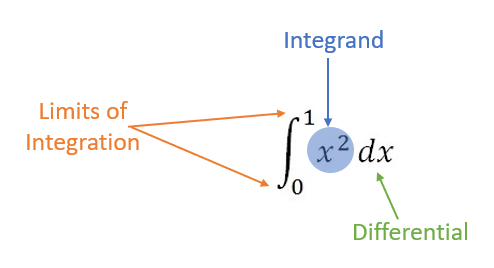
The integrand is a function you want to integrate.
It’s the calculus equivalent of a dividend in basic math, which is a quantity you want to divide up. With the integrand, it’s the quantity you want to integrate.
Examples
In the integral
∫ x2 sin 4x dx,
the integrand is x2.
For (x + 4)3 dx, the integrand is (x + 4)3.
Odd and Even Integrand
The terms “odd” and “even” here don’t refer to positive (+) or negative (-) quantities; they refer to odd functions or even functions. Odd functions are symmetric around the origin, while even functions are symmetric around the y-axis (the vertical axis). These facts are important, because they can help you to solve ugly looking integrals just by considering the shape of a graph.
For example, the following graph is of the function x log(2.125 + x2) e-x2, an odd function (because it’s symmetrical around the origin):
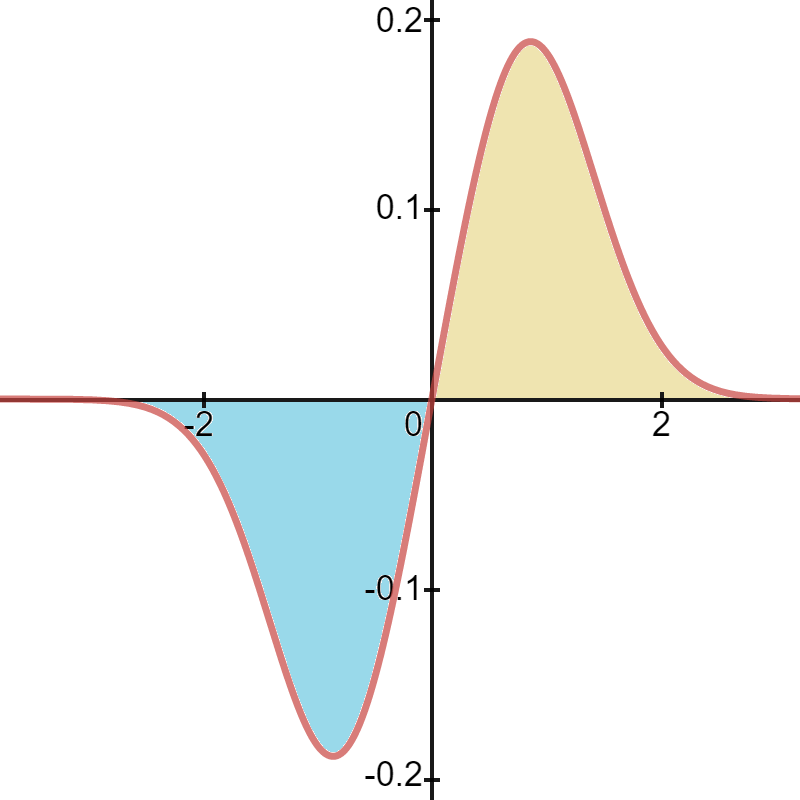
Let’s say you wanted to evaluate the integrand (x log(2.125 + x2) e-x2) over the interval -2 to 2. You could use a calculator, but an easier way is to look at the graph. An integral is really just the area under a curve, so the total area for this integral is zero (because you subtract the area below the curve from the one above, and they are both equal). That fact will hold for all odd integrands, as long as you are evaluating them equidistant from the origin (e.g. -2 to 2, -9 to 9 or -1000 to 1000).
Integrand Function
The term generally refers to a function being integrated in numerical integration, although it’s sometimes informally used in general integration as an answer to the simple question “what function is being integrated?”.
For example, you might want to integrate the cosine function f(x) = cos (x) from π2 to π:
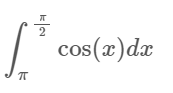
- The integrand function (i.e. the function being integrated here) is f(x) = cos (x).
- The interval is π/2 to π.
Together, these two pieces of information tell you what you’re integrating and where the limits or integration are located.
Integrand Function in Software
You might also come across the function in MATLAB or R.
For example, Yang et al. (2018) refer to the following in a discussion on symbolic line integrals/surface integrals in MATLAB:
f = Vector or Scalar integrand function in x, y, and z
The meaning is the same here, except the authors are stating that the function can be scalar or vector.
In their book, Mastering Scientific Computing with R, Gerrard and Johnson (2015) first show how to solve a problem using the R function integrate(). This function allows you to calculate integrals by adaptive quadrature for functions of a single variable over a defined interval. In order to use the integrate() function, you first have to define it and save it as an integrand object. For a simple example, you would input the function x2 as:
> integrand <- function(x) {x^2}
You can them combine this with the integrand function, setting the lower and upper limits and interval [a, b]:
>integrate(integrand, lower = 0, upper = 4)
21.33333 with absolute error < 2.4e-13 The above example gives the exact solution ∫f(x)dx) = x3 / 3.
References
Gerrard, P. & Johnson, R. (2015). Mastering Scientific Computing with R. Packt Publishing
Hoffman, J. & Frankel, S. (2001). Numerical Methods for Engineers and Scientists, Second Edition. CRC Press.
Yang, W. et al. (2018). Engineering Mathematics with MATLAB. CRC Press.
Desmos Graphing Calculator.
John D. Cook Consulting. Saved by Symmetry. Retrieved December 5, 2019 from: https://www.johndcook.com/blog/2011/03/31/saved-by-symmetry/
Open University. 3.3.3 Multiplication and Division Math Terminology. Retrieved December 5, 2019 from: https://www.open.edu/openlearncreate/mod/oucontent/view.php?id=605§ion=4.3