Contents:
Multivalued Function: Definition
A multivalued function (also called a multiple-valued function) has more than one distinct output for at least one input.
For example, the functions y = √ x and y = -√ x are two separate functions. They can be combined into one multivalued function y2 = x, y, which has two real values when x > 0.
Multivalued Function Examples
Some of the most important multivalued functions in complex analysis are:
- √z,
- n√z,
- √((z-a)(z-b))
- log z,
- za,
- sin-1z,
- cos-1z.
Multivalued functions are not actually functions
These functions work differently from the usual single-valued functions you come across in calculus, and they aren’t your everyday functions (i.e. they are not one-to-one or many-to-one). You can only perform calculus on a part of the function—a branch: the real-numbered part, imaginary part, modulus or argument. The place where these individual parts branch out from each other are called branch cuts. For example, the negative real axis is a branch cut for the two parts of the square root function (y = √ x and y = -√ x).
To complicate things further, these parts themselves might be multivalued. For example, log z has the multivalued imaginary part z1/3.
Branch Point
A branch point is a point “z” where a multivalued function equals zero or infinity. It’s the point where the function’s single-valued branches are “tied” together.
The following image shows what happens to the multivalued logarithm function around the origin:
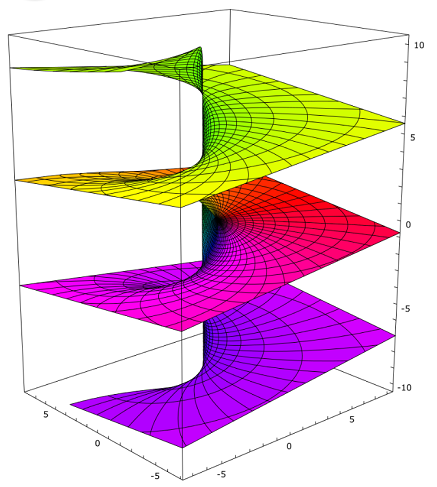
A slightly more technical way of saying the same thing is that a branch point happens when a multivalued function w(z) is discontinuous upon traversing a small circuit around a particular point.
Finding the exact location for a particular function’s branch points can be challenging for uncommon functions. Branch points for some familiar functions are well known.
Branch Points of Specific Functions
The complex-valued root function, w = z1/n and the logarithm function, w = log z, have two branch points: z = 0 and, in the extended plane (a complex plane with a point at infinity attached), z = ∞. As a variable z in this function travels around the point z = 0, it doesn’t return to its original starting point.
Example in Terms of Real-Valued Function
To visualize what happens at a branch point in a multivalued complex function, let’s take a look first at a graph of a real-valued function, y = R(x).
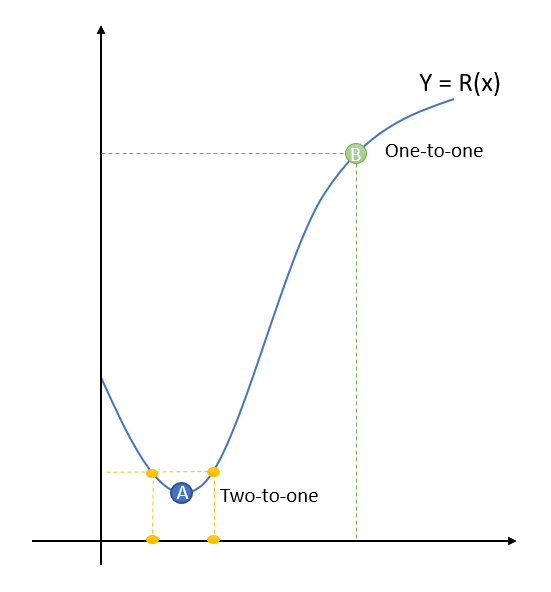
Any point around point “A” (where the derivative is zero) is two-to-one. Any point around point “B” is one-to-one, and has a derivative.
A very similar thing happens with complex functions, except on a 4-dimensional plane.
Why does the function behave strangely around a branch point?
Anywhere there is a derivative on the complex plane, the neighborhoods around the point have one-to-one correspondence, just like the points around B in the real-valued function. But at points like A, where the first derivative is zero, that’s when things get a little strange: the complex function starts to behave like the exponential function zm, orbiting “m” times as fast around the point and creating “m” preimages (preimages are the set of function arguments that correspond to a subset in the range).
If this sounds a little nonsensical, that’s because it is: as an example, the logarithmic function has a branch point of infinity—it’s undefined at that point and has no meaning. So, in a way, the behavior of a function around a branch point has no meaning either!
References
Ablowitz, M. et al. (2003). Complex Variables: Introduction and Applications. Cambridge University Press.
Brand, L. (2013). Advanced Calculus: An Introduction to Classical Analysis. Courier Corporation.
Craig, D. (2007). Complex functions, single and multivalued. Retrieved December 15, 2019 from: file:///C:/Users/brit6/Downloads/multifun.pdf
Haber, H. Branches of Functions. Retrieved December 15, 2019 from: http://scipp.ucsc.edu/~haber/ph116A/ComplexFunBranchTheory.pdf
Jensen, V. et al. (1977). Mathematical Methods in Chemical Engineering. Elsevier.
Knopp, K. “Multiple-Valued Functions.” Section II in Theory of Functions Parts I and II, Two Volumes Bound as One. New York: Dover, Part I p. 103 and Part II pp. 93-146, 1996.
Pham, T. Multivalued functions via Mathematica. Retrieved December 15, 2019 from: http://people.oregonstate.edu/~phamt3/Courses/S19-Math-483-583/MathematicaGuide-4.pdf
Paliouras, J. & Meadows, J. (2014). Complex Variables for Scientists and Engineers: Second Edition. Courier Corporation.
Branch point 3D image: Leonid 2 [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)]