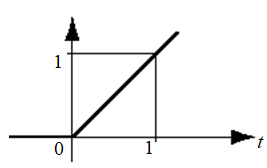
The unit ramp function t(t), is a ramp function with a constant slope of 1. Widely used in signal processing, the function forms a building block for more complex signals.
Expression as an Integral
The unit ramp function is the integral of the unit step function μ(t), so can be expressed as the following integral:
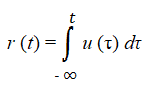
The unit ramp function can also be obtained by integrating the unit impulse function twice.
Values of the Unit Ramp Function
The function can be expressed mathematically as:
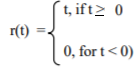
Or, alternatively, by angles. The unit ramp is horizontal with one shift (in an anticlockwise direction) at t = 0 where the function takes on a 45 degree angle to infinity (Singh et. al, 2013).

Shifted Unit Ramp Function
The unit ramp function usually starts at zero. However, it can also shift along the x-axis (in the positive direction). This function is called a delayed ramp function, because of the delay in the start time, at t = a. The function’s values will obviously not be zero, as in the above definition. Instead, the shifted unit ramp is defined as (Bakshi, 2009):
- f(t) = (t – a), for t ≥ a
- f(t) = 0, for t < a.
References
Bakshi, U. (2009). Circuit Theory. Technical Publications Pune.
Singh, S. (2013). Proof of Sp’s… Ramp Function with the Help of Examples. International Journal of Engineering and Innovative Technology (IJEIT) Volume 2, Issue 7, January 2013