Parent Function: Definition, Examples & Graphs

Types of Functions >

What is a Parent Function?

Every function in the Cartesian plane stems from a particular parent function.

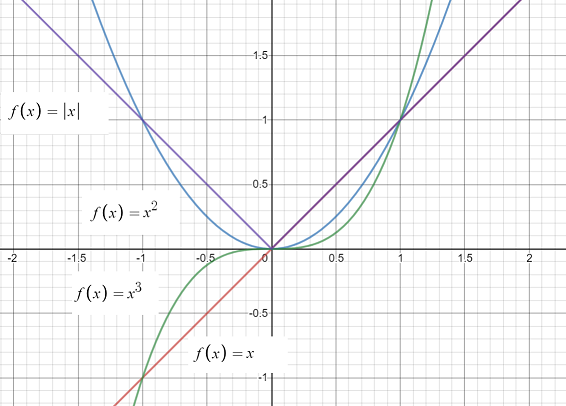
For example, every linear function can be generated from the parent function f(x) = x; Every other possible linear function of the form y = mx + b is a child function of this parent. Together, parent functions and child functions make up families of functions.

To put this another way, every function in a family is a transformation of a parent function. For example, the function f(x) = 2x is the linear parent function vertically stretched by a factor of 2; Instead of the function passing through (1, 1) the graph passes through (2, 1):

Common Parent Function List

1. Absolute Value
2. Constant
3. Cube Root
4. Cubic polynomial
5. Exponential
6. Linear (Identity)
7. Logarithmic
8. Quadratic polynomial

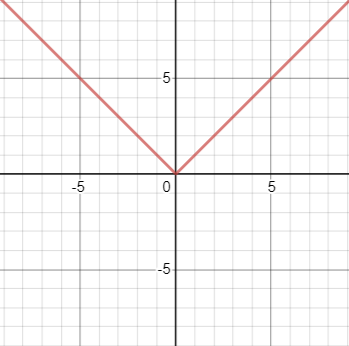
1. Absolute value parent function

The absolute value function is an even function with the parent p(x) = |x|.

Characteristics:

• Domain: (-∞, ∞).
• Range: [0, ∞]; If x ≥ 0, then f(x) = x and if x <0, then f(x) = -x.
• Inverse Function: f(x) = x, for x≥ 0.
• General form: f(x) = a|b(x – h) + k.

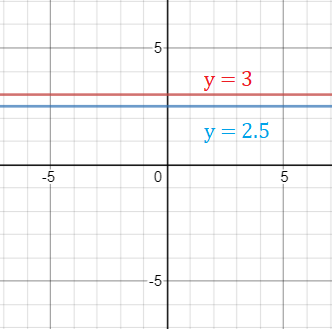
2. Constant Parent Function

The constant function is an even function that has the parent f(x) = c.

The graph depends on the value of c. For example, the following graph shows two constant functions where c = 3 (red) and c = 2.5 (blue):

Characteristics:

• Domain: (-∞, ∞).
• Range: [c, c], where c is a real number.
• Undefined (asymptotic) inverse Function.
• General form: Ay + B = 0

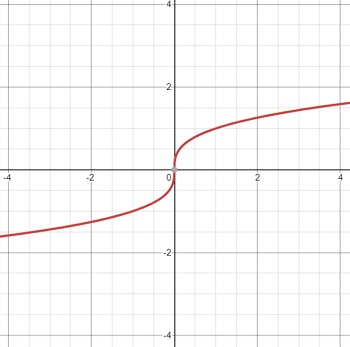
3. Cube Root Parent Function

The cube root function is an odd function that has the parent
f(x) = ∛x.

Characteristics:

• Domain: (-∞, ∞).
• Range: (-∞, ∞).
• Inverse Function: g(x) = x³
• General form: f(x) = ∛√(b(x – h)) + k.

4. Cubic Polynomial Parent Function

Cubic functions are odd functions. The parent is: f(x) = x³.

The cubic parent function is strictly increasing, which basically means it’s always headed upwards.

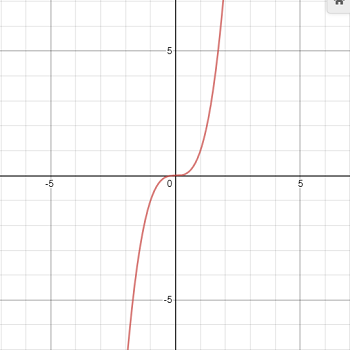
Characteristics:

• Domain: (-∞, ∞).
• Range: (-∞, ∞).
• Inverse Function: g(x) = ∛x
• General form: f(x) = a((b(x – h))³ + k.

5. Exponential Parent Function

The exponential function has no restrictions: inputs can be real numbers or imaginary numbers. The parent function is either f(x) = e^x or f(x) = 10^x.

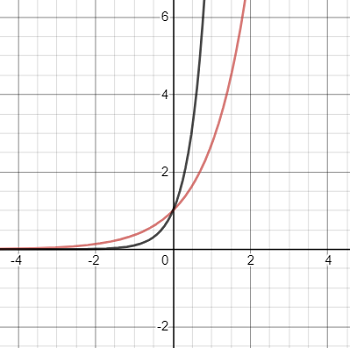
Characteristics:

• Domain: (-∞, ∞).
• Range: (0, ∞).
• Inverse Functions: g(x) = ln(x) or g(x) = log(x).
• General form: f(x) = a 10^{(b(x – h))} + k.

6. Linear function

The linear function is an odd function with the parent:
f(x) = x.

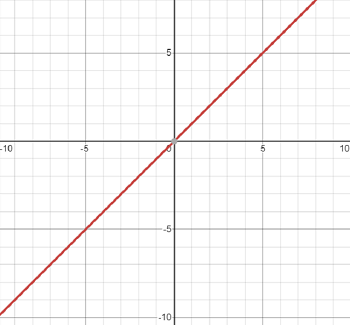
More info: Linear parent functions.

Characteristics:

• Domain: (-∞, ∞).
• Range: (-∞, ∞).
• Inverse Function: g(x) = x.
• General form: y = mx + b (m ≠ 0). Alternative: Ax + By + C = 0 or y – y₀ = m(x – x₀). For an overview of the different forms, see: Standard Form.

7. Logarithmic function

Parent: f(x) = log_bx; Where b is the base.

For example, the parent f(x) = log₂x is different from the parent f(x) = log₁₀x.

The parent function for the natural logarithm function is ln(x).

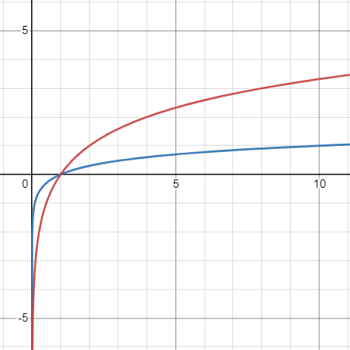
Characteristics:

• Domain: (0, ∞).
• Range: (-∞, ∞).
• Inverse Function: g(x) = 10^x or g(x) = e^x
• General form: f(x) = a log(b(x – h)) + k.

Quadratic or Square Function

Parent: F(x) = x²

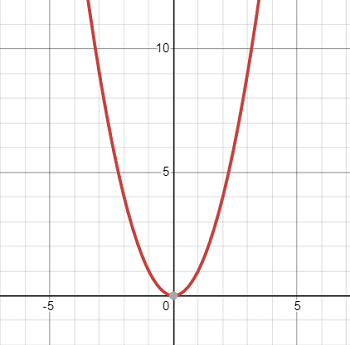
Characteristics:

• Domain: (-∞, ∞).
• Range: (0, ∞).
• Inverse Function: g(x) = √x
• General form: Ax² + By + Cx + D = 0.

References

Desmos Graphing Calculator.
UF Library of Functions. Retrieved March 11, 2021 from: https://xronos.clas.ufl.edu/mac1140nowell/PrecalculusXourse/graphing/parentFunctions.
Harold’s Parent Functions “Cheat Sheet” (2016). Retrieved March 11, 2021 from: https://people.clas.ufl.edu/srnatkins/files/ParentFunctionChart.pdf