Contents (Click to skip to that section):
- What is an X-Intercept?
- What is a Y-Intercept?
- How to Find Intercepts with Factoring & Quadratic Formula.
X-Intercept (Definition)
The x-intercept is the point where the graph of the plotted line crosses the x-axis. On the graph below, the plotted line crosses the x-axis at x = 5.
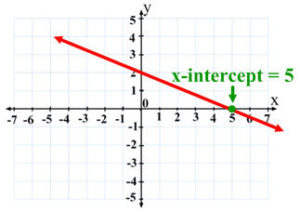
Eyeballing the graph isn’t an exact method. For example, in the graph above, the actual x-intercept could fall somewhere between 4.9 and 5.1. A more precise method for finding the intercept is to use the equation for a line. The universal formula for every straight line, a linear equation, is:
Where:
- m = the slope of the line (its steepness). The slope is found by dividing the change in y-value by the change in x-value,
- b = the y-intercept,
- x = the x-value.
You will often need to find the value of the x, given values for m and b. For that, you’ll need to use a little algebra.
Example: Finding the X-Intercept
Example question: What is the x-intercept of the equation y = 3x – 1?
Step 1: Set y to O.
0 = 3x – 1
Step 2: Add 1 to each side:
0 (+ 1) = 3x – 1 (+ 1)
1 = 3x
Step 3: Divide both sides by 3:
1 (/3) = 3x (/3)
⅓ = x
The x-intercept for the above equation is 1/3.
Quadratic Equations
Another case where you will come across the x-intercept is in dealing with quadratic functions. A quadratic equation has two solutions; The line is in the form of a parabola, which means that there will be two x-intercepts. The standard quadratic equation is:
y = ax2 + bx = c
In this example, you’ll need to use the quadratic formula to find the x-intercept.
Next: Quadratic Formula
Y-Intercept (Definition)
The y-intercept is the point where a graph crosses the y-axis. On the graph below, the plotted line crosses the y-axis at y = 3:
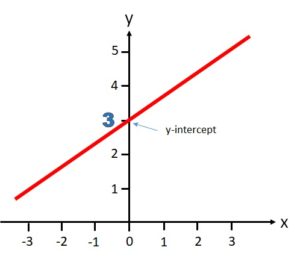
More Examples
To find the y-intercept on a graph, just look for the place where the line crosses the y-axis (the vertical line).
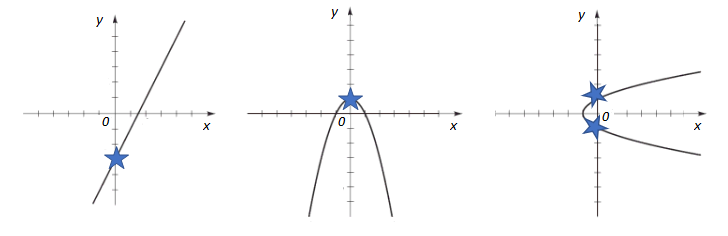
Note that you can have more than one y intercept, as in the third picture, which has two y intercepts. In calculus, you won’t see more than one y intercept, because it creates a major issue called “one to many.” In other words, your graph fails to represent a function (it might be a valid equation, but in calculus, you have to have functions in order for the math to work!).
Y-Intercepts in Linear Equations
The universal formula for every straight line, a linear equation, is:
Where:
- m is the slope of the line (its steepness).
- b is the y-intercept.
Sometimes, the intercept can be found just by looking at the value in the b position. For example, in the linear equation y = 2x – 2, the line will intersect the y-axis at -2.
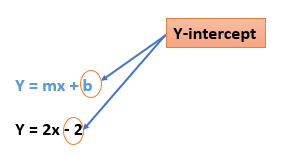
You will often need to calculate the value of b, however, given values for m and x.
Example: Finding the Y-Intercept
Example question: At what point on the y-axis will a line with a coordinate point (1,1000) and a slope of 750 pass?
Step 1: Insert each of the given numbers into the standard linear equation:
- y = mx + b
- 1000 = 750(1) + b
- 1000 = 750 + b
Step 2: Solve for b using algebra.
- Subtract 750 from both sides: 1000 (-750) = 750 (-750) + b
- 250 = b
The y-intercept of the line is 250. The plotted line will pass through the y-axis at point 250.
Y-Intercept in a Quadratic Equation
Another case where you will encounter y-intercept is in dealing with quadratic equations. In a standard quadratic equation:
y = ax2 + bx + c
The intercept is represented by point c. In the following equation:
y = 2x – x + 4
the y-intercept is 4.
For more information on working with quadratic equations check out Quadratic Formula.
How To Find Intercepts
Intercepts are where the function crosses the x-axis (the x-intercept) and the y-axis (the y-intercept). There are several ways you can find intercepts:
- The guess and check method,
- Factoring,
- The quadratic equation,
- Finding the solution using a graphing calculator.
Guess and check works well for very simple equations like y = x + 2, but you’ll rarely be dealing with simple equations in calculus. Most graphing calculators have the ability to solve for intercepts (you can find a simple online calculator here). However, in many cases (especially in elementary algebra or pre-calculus), you’ll need to find the solutions algebraically. If you don’t have strong algebra skills, you might run into difficulties. However, referring to a graph can help, so can calculators like this one (which factors for you).
How to Find Intercepts in Calculus: Factoring Example
Example problem 1: Find the intercepts of the function
- y = x3 – 9x.
Step 1: Find the x-intercept(s):
- Set the function equal to zero: x3 – 9x = 0
- Factor: x(x – 3) (x + 3) = 0,
- so x = 0, x = -3, x = 3.
Written as ordered pairs, the x-intercepts are (-3, 0), (0, 0) and (3, 0).
Step 2: Solve to find the y-intercept:
- x3 – 9x = y
- (0)3 – 9(0) = y
- y = 0
How to Find Intercepts in Calculus: Quadratic Formula Example
Find the intercepts of the equation y = x2 – 2x – 1.
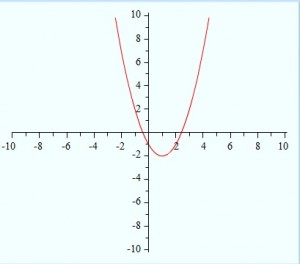
Step 1: Set x to 0 in your function to find the x-intercept:
02 – 2(0) -1 = -1.
Written as an ordered pair, the x-intercept is (0, -1).
Step 2. Set y to 0 and then solve to find the y-intercept:
- 0 = x2 – 2x -1 (setting y to zero)
- x = -1± √ 2 (using the quadratic formula to solve)
- Therefore, there are two intercepts at (-1- √ 2, 0) and (-1 + √ 2, 0).
Tip: Check your solutions on a graphing calculator if you can, to see if they make sense. Looking at this particular graph, we can clearly see that there are two points where the graph crosses the x-axis and one point where it crosses the y = axis.
References
Stewart et al. (2003). College Algebra. Cengage Learning.