Increasing and Decreasing Functions (Contents):
- What is an Increasing Function?
- Decreasing Function / Monotonically Decreasing
- Non Increasing Function
- Non Decreasing Function
What is an Increasing Function?
Simply put, an increasing function travels upwards from left to right. In other words, as the x-values increase, the function values decrease.
Mathematically, an increasing function is defined as follows:
f is increasing if every x and y in A, x ≤ y implies that f(x) ≤ f(y)
Where “A” is the set of real numbers.
Strictly Increasing Function
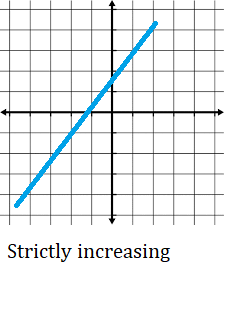
A strictly increasing function always increases, over its entire domain. It isn’t allowed any dips or plateaus where the function stays constant for even a short time.
For example, your function might increase everywhere, then suddenly, at infinity, it might drop off into an abyss. If that happens, the function is still increasing—everywhere except for one tiny point at infinity—but it isn’t strictly increasing.
Mathematically, a strictly increasing function is defined as follows:
f is strictly increasing if every x and y in A, x < y implies that f(x) < f(y)
Note that this definition only differs slightly from the first definition, by a less than (<) rather than a less than or equal to symbol (≤). The “equal to” part of the above definition allows for the function to remain constant for periods of time, whereas the inclusion of just “less than” here does not allow for any constant periods.
Increasing and Decreasing Functions: What is Weakly Increasing”?
The term “weakly increasing” is sometimes used to define a function that isn’t strictly increasing. For example, Dartmouth University defines it as:
“A function f is weakly increasing on an interval I if f(b) ≥ f(a) whenever b > a for all points a and b in I that are in the domain of f.”
The Problems with Weakly Increasing
The above definition is basically stating that as the function input increases (i.e. the x-values travel from left to right along the number line), the output also increases, or stays constant. Technically, that means the function could always stay constant. In other words, “weakly increasing” could describe a function that increases, stalls, then increases again, or it could describe a constant function: one that doesn’t increase at all! To put that another way: Weakly increasing does not mean that the function is increasing.
To show you what this looks like on a graph, this function is weakly increasing:
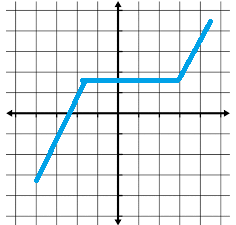
As you can see, the center part of the function is flat. It isn’t increasing, and can’t even be described as even weakly increasing. As for the rest of the function, it’s certainly increasing, but at a fairly fast pace (i.e. it isn’t “weak” here either!).
Alternatives to Using the “Weakly”
The problems with the above graph are one good reason why you should probably avoid using the term “weakly increasing” at all. Instead, consider:
- Using the term “ascending” instead (Dijkstra, 2015).
- Defining your function in parts (i.e. defining the parts that are increasing and also defining the parts that are constant).
Increasing and Decreasing Functions: How to Prove it’s an Increasing Function
Perhaps surprisingly, you can’t just look at a graph and say it “looks increasing.” That’s because, say you have a graph that’s headed straight down. You can’t say for sure that there isn’t a very tiny point where it does something strange (see strange functions or pathological functions for some examples!). The only way to prove that you have an increasing function over the whole domain is to find the first derivative. The function is increasing wherever there is a positive first derivative.
What is a Decreasing Function?
A decreasing function has a downward slope over the entire graph; as you move from left to right on the x-axis, the graph goes downward. In other words, as the input variable (x) increases, the output (y) decreases.
Formal Definition
More formally, a decreasing function is defined as decreasing over the domain a ≤ b, if any two points x1, x2 (where a ≤ x1 ≤ x1 ≤ b) result in function outputs f(x1) > f(x2).
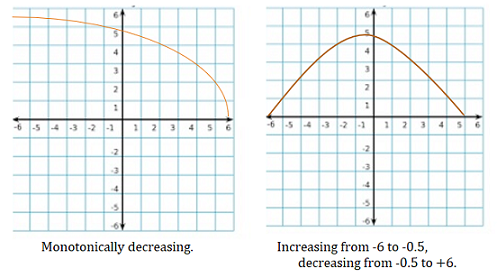
A function can be decreasing at a specific point, for part of the function, or for the entire domain. A monotonically decreasing function is always headed down; As x increases in the positive direction, f(x) always decreases.
The point where a graph changes direction from increasing to decreasing (or decreasing to increasing) is called a turning point or inflection point. Turning points can be local maxima (high points) or local minima (low points). If you are graphing the entire function (i.e. over the whole domain), the single highest point is the absolute maximum, and the single lowest point is the absolute minimum.
How to Find Out if a Function is Decreasing
The first derivative test can be used to determine if the function is decreasing. A function is decreasing at point a if the first derivative at that point is negative. If the first derivative is always negative, for every point on the graph, then the function is always decreasing for the entire domain (i.e. it’s monotonically decreasing).
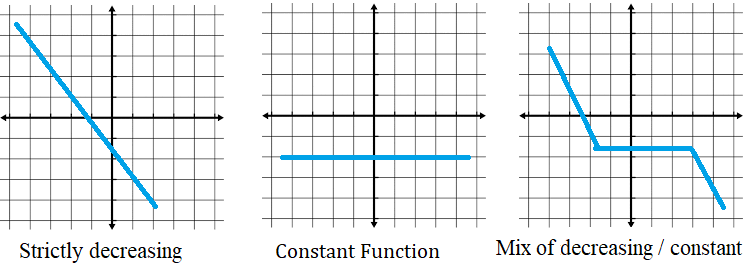
Increasing and Decreasing Functions: What is a Non-Increasing Function?
A non-increasing function doesn’t ever increase. It can be a:
- Strictly decreasing function (i.e. a function that decreases constantly),
- Constant function,
- Mix of decreasing and constant segments.
A non-increasing function is defined mathematically as one where:
x1 > x2 ⇒ f(x1) ≥ f(x1).
In other words, take two x-values on a specified interval (which could be the entire function); If the function’s output at the first x-value is less than or equal to the function output at the second, then the function is non-increasing. However, note that it’s possible for the function to increase between the two points; There are two discrete variables x1 and x2 and the function could be doing something strange in between those point (for example, it could be a wave, like the sine function). This issue with the definition can be averted in a couple of ways.
- Specify the domain in the definition. For example, for all x1, x2 ∈ X.
- Use derivatives: A function f is non-increasing on the interval [a, b] if and only if the first derivative is not positive anywhere. The difference f(x + h) – f(x) is not positive for h, no matter how small the difference.
Using Derivatives to Define Non-Increasing Functions
As stated in the above definition, a non-increasing function has a non-positive first derivative. What this means for finding out if a function is non-increasing, is to perform a first derivative test. The test can be performed on an entire function, or parts of a function.
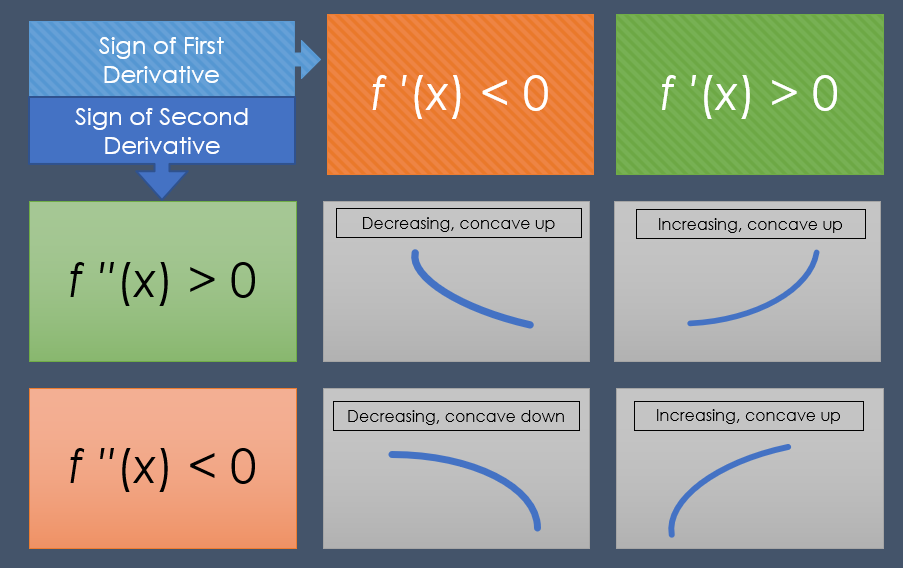
The following table shows how the first derivative test (f′) and the second derivative test (f′′) can tell you about a function’s direction and shape. The idea is that you find the first derivative for the function, find the second derivative, and take note of the signs of the two derivatives (positive or negative).

Non Decreasing Function
A non-decreasing function is a function that doesn’t decrease. It can be an increasing function, a constant function, or a mixture between the two.

More Formal Definitions
A non-decreasing function is sometimes defined as one where x1 < x2 ⇒ f(x1) ≤ f(x2).
In other words, take two x-values on an interval; If the function value at the first x-value is less than or equal to the function value at the second, then the function is non-decreasing. However, this fairly simple definition comes with a problem: it’s possible for the function to decrease somewhere in between the two points. In order to fully define non-decreasing functions, we need to think of them in terms of derivatives.
The function f is a non-decreasing function on the closed interval [a, b] if and only if the first derivative (f′) ≥ 0 on (a, b). This addresses the problems with the simpler definition above, because the definition covers all possible points in the interval. Also, this seems to make intuitive sense, because a negative first derivative would indicate that the function is decreasing at some point in the interval. Obviously, if the function is decreasing somewhere on the interval then it’s not a non-decreasing function.
Increasing and Decreasing Functions: Non-Decreasing on an Interval
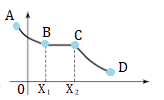
A part of a function can be non-decreasing, even if the function appears to be decreasing in places. This is true if, for two x-values (x1 and x2, shown by the dotted lines):
- x1 < x2 ⇒ f(x1) ≥ (x2).
- For segments AB and CD (the decreasing parts): x1 < x2 ⇒ f(x1) ≥ f(x2).
- For segment BC: While x1 < x2 ⇒ f(x1 = f(x2.
Increasing and Decreasing Functions: References
Dijkstra, E. (2015). Largely on nomenclature. Retrieved December 14, 2019 from: https://www.cs.utexas.edu/users/EWD/transcriptions/EWD07xx/ewd768.html
Gasteren, A. (1990). On the Shape of Mathematical Arguments. Springer Science & Business Media.
Review: Properties of Graphs – 9/14/16. Retrieved December 14, 2019 from: https://math.dartmouth.edu/~m1f16/MATH1Docs/Dennis%20graph%20properties%20Review.pdf
Karshon, Y. APPLICATIONS OF DERIVATIVES, CONTINUED. Retrieved December 12, 2019 from: http://www.math.toronto.edu/karshon/courses/mat157/notes.1811-applications2.pdf
Kai-Chieh, C. Untitled homework answers. Retrieved November 20, 2019 from: https://math.berkeley.edu/~kaichieh/MATH1A/Hw/18.pdf
Mavron, V. & Phillips, T. (2007). Elements of Mathematics for Economics and Finance. Springer Science & Business Media.
Rahi. Concepts of Functions and Calculus.
Chapter 8: Functions and One-to-One. Retrieved December 13, 2019 from: http://mfleck.cs.illinois.edu/building-blocks/version-1.3/functions-one-to-one.pdf
Singh, A. (2019). Optimization for ML. Retrieved November 20, 2019 from: https://www.cs.cmu.edu/~aarti/Class/10315_Fall19/recitations/recitation_3.pdf