The sinc function, or cardinal sine function, is a symmetric, wavelike function denoted by sinc(x). It is sometimes called the sampling function.
There are two different definitions for the function: unnormalized and normalized. Which one you use depends upon which field you’re working in.
- The unnormalized sinc function is usually used in mathematics. This sine wave decays in amplitude as 1/x:
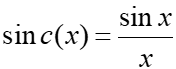
- The normalized sinc function is used in signal processing (which includes radio transmissions and sound recording) and information theory:
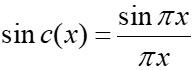
Note that in signal processing and connected fields, you’re usually working with the variable “time(t). Therefore, you’ll see this formula written out with “t” in place of the “x”.
Graph of the Functions
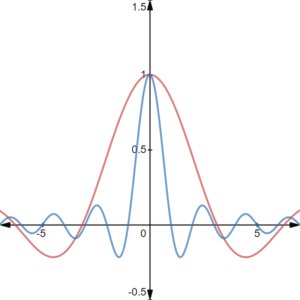
This is a symmetrical function: Sinc(x) = Sinc (-x) which oscillates like its close relative sin(x):
Definite Integrals, Limit and Zeros of Sinc Functions
A similarity that both functions share is the same limit at x = 0, which is 1. One major difference (other than the slightly different formulas) is that the “normalized” version has been normalized so that the definite integral (i.e. the area under the graph) equals 1; The unnormalized sinc function’s definite integral is π. Another difference: the normalized version crosses the x-axis at integers.
While the normalized sinc function has the rather handy feature of it crossing the x-axis at non-zero integers, that makes it not practical for many purposes. That’s because the function has zeros for all integer inputs, except for zero. Depending on what you’re trying to calculate, that could be a severe limitation. However, it’s possible to multiply the function by a window function: one that has non-zero values in a finite range. Together, the functions are called a Windowed Sinc Function.
References
Bannore, V. (2009). Iterative-Interpolation Super-Resolution Image Reconstruction: A Computationally Efficient Technique
Desmos Calculator.
Math Review. Retrieved November 26, 2019 from: https://www.cse.unr.edu/~bebis/CS474/Lectures/MathReview.ppt
Signal processing toolbox: Sin c function. Retrieved November 26, 2019 from: https://edoras.sdsu.edu/doc/matlab/toolbox/signal/sinc.html