An accumulation function gives the area under the curve of a function between a fixed value a and a variable. While it’s common just to see “x” as the upper limit of integration, you can have one or more variable expressions for the upper limit. For example, instead of “3” as a limit of integration, you might have x2.
A definite integral is evaluated between specific values a and b, but when “b” is replaced with a variable, the integral is no longer “definite”. Instead, the definite integral becomes a function in x. Essentially, it’s a different way of looking at an antiderivative from the point of view of Riemann sums.
They are called “accumulation” functions because they represent the accumulation of the area beneath a curve.
Example of an Accumulation Function
As an example, let’s say the accumulation function was [1]
Values for x and 2e-cos(x) – 2.5 vary simultaneously, accumulating area as x-varies:
Graph of an Accumulation Function
The graph of an accumulation function F(x) measures the area under a graph of y = f(t) over the interval a < t < x. The lower limit a is fixed but the upper limit x is allowed to vary. You’ll see “t” used here to indicate the points on the graph; We can’t use x as that shows the position along the horizontal axis.
The following graph shows a function (left) and a table of accumulation function values (right) [2].
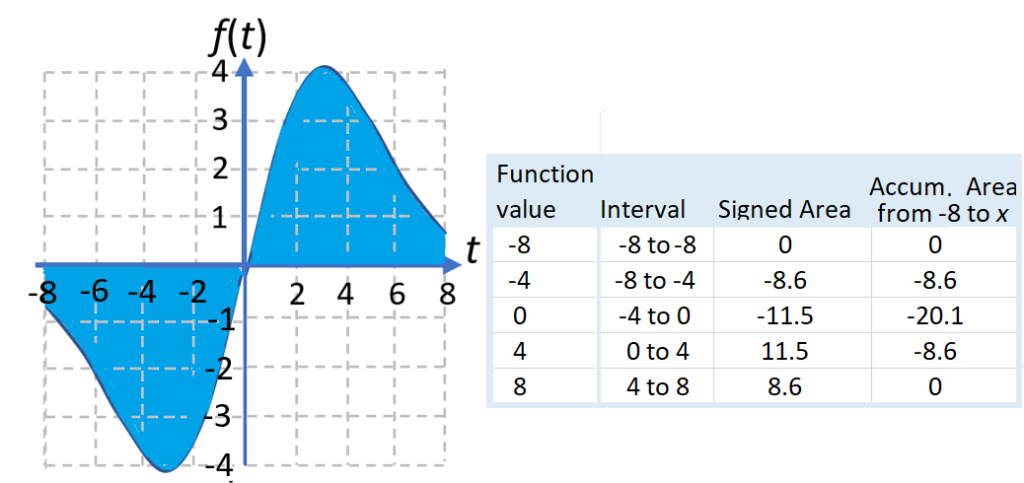
Remember that when you’re calculating area with integrals, areas under the horizontal axis are negative; You subtract negative areas from positive ones, which is why the total area is zero.
Evaluate an accumulation function just like you would any other definite integral: plug in an x-value. The graph of an area accumulation function can be found by plotting for particular values of x.
References
[1] Carlson, M. & Rasmussen, C. (2008). Making the Connection: Research and Teaching in Undergraduate Mathematics Education. Mathematical Assn of America.
[2] Torre, D. et al. (2011). Calculus Concepts: An Informal Approach to the Mathematics of Change. Cengage Learning.