What is the Vertical Line Test?
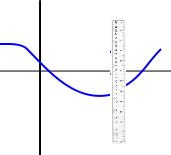
The vertical line test is an easy way to see if you have a function just by looking at a graph.
Note: If you don’t know what a function is, you may want to read the function definition first.
Contents:
Vertical Line Test: Steps
The basic idea:
Draw a few vertical lines spread out on your graph.
- If each line crosses the graph just once, the graph passes the vertical line test. It is a function.
- If a vertical line can cross a graph more than once, then the graph does not pass the vertical line test. It is not a function.
Step 1: Draw the graph.
Step 2: Place a ruler vertically (straight up and down) on your graph. Move the ruler left to right along the length of the graph. Look for any place where the ruler crosses through the equation. If the ruler crosses the graph once, that’s fine. If it crosses it two or more times, then that’s not a function. To put that another way, if any x-value on the graph has more than one y-value (output), then the equation is not a function.
Note that the vertical line is allowed to miss the graph (see the semicircle picture below), it just can’t hit it multiple times.
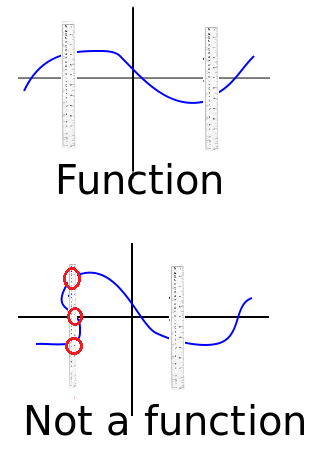
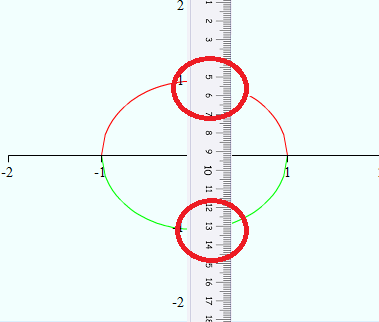
Are Circles Functions?
Circles are never functions, because each x-value has two y-values; Place a ruler vertically anywhere on the graph and the graph will cross the ruler twice.
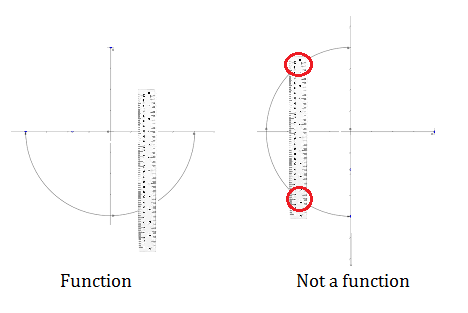
Different rules apply to semicircles. If the semicircle’s peak points up (as shown in the left image), it’s a function. If it points to the left or right, then it isn’t a function.
Note that on the right, the ruler would completely miss the graph if it were placed in the first or fourth quadrants (i.e. to the right of the y-axis). That’s not however, what causes it to not be a function. The important part is the ruler crosses the graph twice; we really don’t care about blank space.
Are Parabolas Functions?
Parabolas follow the same rule as semicircles. Vertical parabolas (where the peak stretches along the y-axis) are functions. However, horizontal parabolas (i.e. one where the peak stretches out along the x-axis) are not functions:
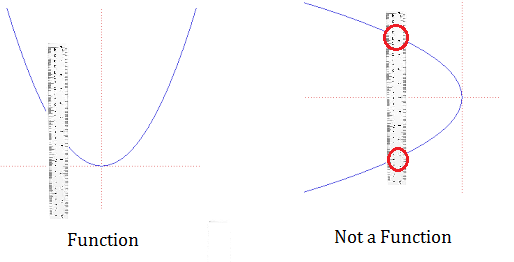
Parabolas and circles both have y2 in their equations, so this provides a clue: any equation that has y2 has a high chance of not being a function.
Inverse Trig Functions
As a general rule, inverse trig functions are actually not real functions, with one small exception. As an an example, sin is a function (shown in green in the image below). But if you create inverse sin by reflecting the function over the line y = x, you get a vertical wave that isn’t a function because it doesn’t pass the vertical line test. However, if you take a small piece of inverse sin that passes the vertical line test, then that small piece is a function.
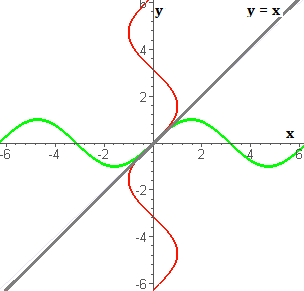
![]()
Historical Notes
While the word function goes back to Leibniz in 1694 (Burnett, 2005), the idea of a function only being a function if it meets the vertical line test has only come about in recent history. Early calculus authors thought that some graphs were functions, although today they are not considered functions. For example, Silvanus Thompson, in his seminal work Calculus Made Easy (1914), considers this graph a function. However, it clearly fails the vertical line test:
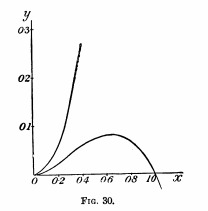
The original term may have stemmed from the vertical line test in physiology, which was defined as:
“The Vertical Line Test”: In good posture, the long axis of the trunk is a vertical line and the long axis of the neck and head taken together is also a vertical line. An imaginary line dropped from the front of the ear to the forward part of the foot will parallel the long axes of these segments of the body. In poor posture these axes do not form one continuous vertical line but are broken into several zigzag lines. (Military Training Commission, 1917, p.49)”
One of the earliest algebraic uses of the term appeared in The Florida Program of Curriculum Revision: General Plans and Organization (1931). The mention is brief, and it’s unlikely the idea of a mathematical vertical line test originated here. However, it does suggest the vertical line test might have been used in algebra before 1931.
A few sporadic mentions of the test are found in later texts, such as Mathematics for High School: Intermediate Mathematics: Commentary for Teachers, Volume 1 (1959). In 1970, Buchman and Zimmerman state that “Graphically…a relation is a function if and only if no vertical line meets the graph of the relation at more than one point. This is sometimes called the vertical line test.”
Next: Horizontal Line Test
thanks = )
good work