Contents:
What is a Local Minimum?
A local minimum is the lowest point on a function, given a certain range.
Since every function has high points and low points, it’s essential to know how to find them. But, since there can be infinitely many of these points, we can choose a segment of the function and solve the ones in there. This is done by using derivatives and simple arithmetic. Here, we’ll focus on finding the local minimum.
We will take this function as an example:
f(x)=-x3 – 3x2 + 1
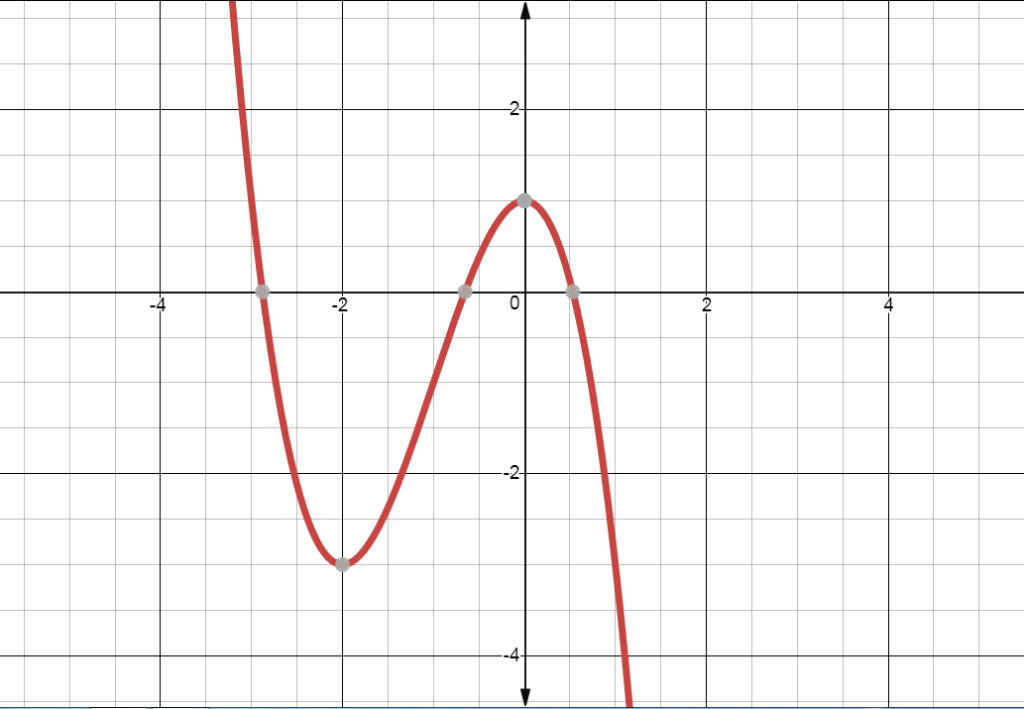
This function has only one local minimum in this segment, and it’s at x = -2.
1. Finding the local minimum using derivatives
Step 1: Find the first derivative of the function. You will get the following function:
f′(x) = -3x2 -6x
If you’re not sure how to get that derivative, see: The Power Rule: How to Differentiate Exponents
Step 2: Find the solution for which this new function, f’(x)—the one you found in Step 1— is equal to zero. This means that you’ll take the equation that you got above, and set it to be equal to zero.
-3x2 – 6x = 0
Step 2: Use basic algebra to solve for x. The values will be x = 0 and x = -2.
The above graph shows us that x =-2 is the lowest point in this area. The other value x = 0 will be the local maximum of this function.
Here, it’s easy to see what the local minimum will be, even without solving.
2. Use the Second Derivative
Another way to find it is by using the Second Derivative Test. This means that you differentiate the original function twice. After you do this, the result will be:
f ′′(x) = -6x – 6
Replace the values that you found earlier (x = -2 and x = 0) in this function.
x =-2:
f ′′(-2) = -6*(-2) – 6
f ′′(-2) = 6
The solution, 6, is a positive number. This means that x =-2 is the local minimum of the function.
The Second Derivative Test tells us that if the result we get is positive, then the initial number used will be a place where there is a local minimum. If the result is negative, then the value we used will be the local maximum. In this case, the maximum would be in x = 0 (f’’(0) = -6).
Global Minimum
An absolute minimum (also called a global minimum) is the lowest point in a function. If you graph the function over every point in the domain, the absolute minimum is simply the lowest point on the graph.
If the function was The Earth, the absolute minimum would be the Mariana trench. By the same token, the absolute maximum in this example would be Mount Everest.
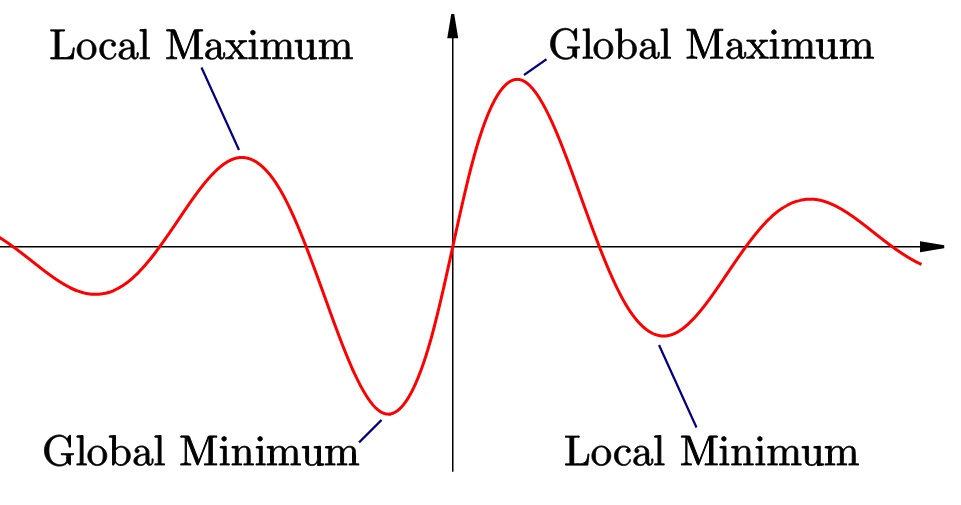
Global vs. Local Minimum
A function can have several low points, but only one absolute minimum. In our “Earth” example, the Mariana trench is in the Pacific. Any other low points (like the Arctic Ocean’s Eurasian Basin or the Indian Ocean’s Java Trench) are local minimums; They are the low point in a particular area. Simply put, the global minimum is the lowest of all local minimums.
The following image is of mean house prices over time for Atlanta and San Francisco (from the Federal Reserve Board).
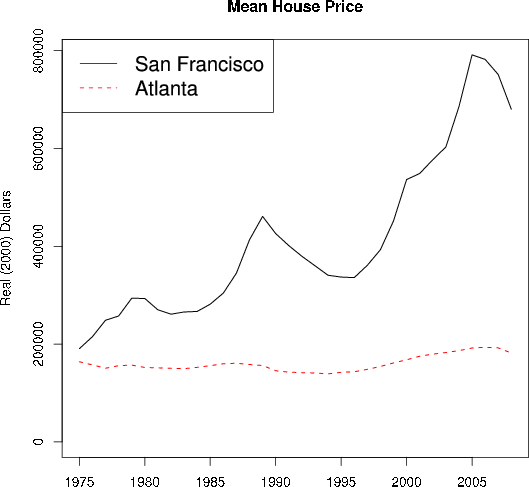
The lowest trough happened in 1975, to the left of the graph. That’s our global (absolute) minimum. However, let’s say you were studying the 20 year period from 1985 to 2005. The low point would be 1985; Because it’s only taking a look at a small part of the data—a localized area— it’s called a local maximum.
The Unbounded Problem
It’s impossible to find an absolute/global minimum for an unbounded function. If a function is unbounded, a mountain could be infinitely high, or infinitely low. In real life, (almost) everything is bounded. Mountains are bounded from 486 ft to 29,035 feet. People are bounded from 21.51 inches (source) to 8 ft 2.8 in. In the classroom though, you might be stuck with a wide range of theoretical function with limits to infinity. The only way you could find a global minimum for an unbounded function is to give it an artificial boundary or limit, in which case it isn’t a global minimum (it would be a local minimum instead).
References
Paciorek, A. (2011). Supply Constraints and Housing Market Dynamics. Article posted on the Federal Reserve website. Retrieved December 7, 2018 from: https://www.federalreserve.gov/pubs/feds/2012/201201/
Desmos graph. (2018). Retrieved from https://www.desmos.com/calculator
Finding Local Maxima and Minima by Differentiation. (2018). Retrieved from https://www.youtube.com/watch?v=pvLj1s7SOtk