A one to one function is a relation that preserves “distinctness”; Every unique member of the domain is mapped to a unique member of its range. Sometimes this type of mapping is called injective.
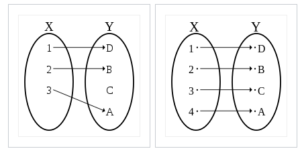
Both images below show injective functions. Notice that each element in X is mapped to a distinct element of Y.
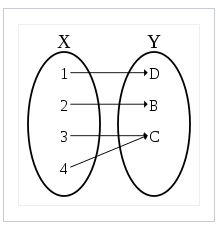
The image below is not this type of mapping. Two distinct elements of X (3 and 4), are mapped to the same element of Y (C).
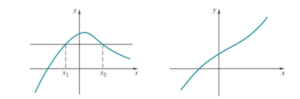
The Horizontal Line Test for a One to One Function
- One easy way of determining whether or not a mapping is injective is the horizontal line test.
Graph the function. - Draw a horizontal line over that graph.
- If any horizontal line intersects the graph of the function more than once, the function is not one to one.
But if there isn’t any straight horizontal line that can be drawn to cross the function more than once, the function is one to one.
Below are images of two different mappings. On the first graph, you could draw a horizontal line that cuts through the hump and crosses the mapping twice. On the second graph, though, there is no way we can draw a horizontal straight line that crosses twice. The function in this second graph is therefore one to one.
Properties of One to One Functions
Here are some useful properties of injective functions:
- If two functions f and g are both one to one, so is f · g.
- If g · f is one to one, f is as well.
- If f is injective, it has an inverse function (a function that undoes it).
References
He, Jiwen. Inverses and More. Lecture 1, Section 7.1 Notes. Retrieved from https://www.math.uh.edu/~jiwenhe/Math1432/lectures/lecture01_handout.pdf
Oldham, K. (2008). An Atlas of Functions. Springer.
University of Toronto Math. Preparing for Calculus: Functions and Their Inverses. Retrieved from https://www.math.toronto.edu/preparing-for-calculus/4_functions/we_3_one_to_one.html on June 15, 2019.