Contents:
Calculus of Variations
Calculus of variations is, loosely speaking, the study of extreme values—the optimization of certain quantities over sets of functions. More technically, it’s the mathematical analysis of nonlinear minimization principles on infinite-dimensional function spaces (Olver, 2021). The field can also be described as a tool where partial differentiation equations can be reformulated as minimization problems.
Calculus of variations can answer questions like: what is the shortest line that connects point A to point B? The solution isn’t always a straight line. For example, let’s say a lifeguard (at point A) is trying to reach a surfer in the ocean (at point B). The lifeguard’s speed on the sand is greater than their speed in the water, which means the optimal line is made up of two line segments: one on the sand, and one in the water. This optimal path satisfies Snell’s law, represented by the equation:
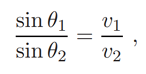
Ordinary Calculus vs. Calculus of Variations
With “ordinary” calculus, the focus is on real functions, which map real numbers to real numbers. For example, the cosine function maps the real number line to the closed interval [-1, 1]. With calculus of variations, the focus shifts to functionals: objects that map functions, instead of numbers, to the real number line. More generally speaking, the quantity S[g] is a functional of g(x) in the interval [a, b] if it depends on every value of f(x) in [a, b].
For example, the functional:
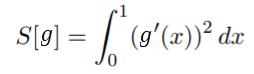
maps the real function g to a real number S[g] (OU, 2016).
Malliavin Calculus
What is Malliavin Calculus?
Malliavin calculus, also called the stochastic calculus of variations, extends calculus of variations from deterministic functions to stochastic (random) processes. More specifically, it differentiates random variables defined on a Gaussian probability space (usually a Wiener space) with respect to underlying noise [1]. These processes have infinite variation, so are not differentiable with traditional calculus tools. In addition, the calculus can integrate random variables using integration by parts.
Malliavin calculus was originally developed by Paul Malliavin in 1976, who used it to to study the smoothness of solution densities of stochastic differential equations. The calculus was further used to investigate regularity properties of the law of Wiener functionals and solutions of stochastic differential equations [2], with further contributions by Bismut, Stroock, Watanabe and others. It is widely used in mathematical finance and financial engineering as well as the study of stochastic partial differential equations.
A Useful but Challenging Calculus
The major downside to Malliavin calculus is that is considered by many to be highly technical and theoretical. This should come as no surprise, as it took centuries for mathematicians even to consider the idea that the integral of random process could possibly exist (in fact, a Lebesgue integral of ∫ f dg cannot exist if g is of infinite variation). Therefore, special tools beyond the “usual” calculus are required, which means a large investment of time to understand how the calculus works. For example, the central tool of Malliavin calculus is the following integration by parts formula [3]:
Suppose that (Ω, F, P) is a probability space and F, G: Ω → R are integrable random variables. The integration by parts formula IP (F; G) holds true if there is some random variable H(F; G) such that
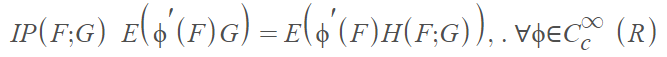
Where C∞c is the space of infinitely differentiable functions with compact support.
The integration by parts formula IPk (F; G) holds true if there is an integrable random variable Hk(F; G) so that
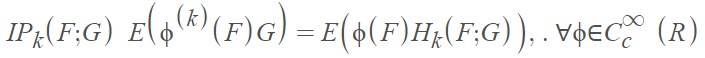
In order to grasp the fundamentals, you have to have some knowledge of calculus (particularly differential equations) and predicate logic as well as a background in financial engineering or other practical application.
Malliavin Calculus: References
[1] Hairer, M. (2021). Introduction to Malliavin Calculus. Retrieved August 27, 2021 from: http://www.hairer.org/notes/Malliavin.pdf
[2] Nualart, D. (1995). The Malliavin Calculus and Related Topics, Springer-Verlag.
[3] Bally, V. (2003). An elementary introduction to Malliavin calculus. [Research Report] RR-4718, INRIA.
Other References
Olver, P. (2021). The Calculus of Variations. Retrieved February 1, 2021 from: https://www-users.math.umn.edu/~olver/ln_/cv.pdf
OU (2016). Introduction to the calculus of variations. Retrieved February 1, 2021 from: https://www.open.edu/openlearn/ocw/pluginfile.php/1118521/mod_resource/content/3/Introduction%20to%20the%20calculus%20of%20variations_ms327.pdf