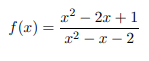Quotient Rule & Function: Definition, Examples

Copy

Contents:

  1. What is the Quotient Rule?
  2. Quotient Function
  3. The Quotient Function in Excel

Related article:
What is the Difference Quotient?

The Quotient Rule

The& quotient rule is used to differentiate functions that are being divided. The formal definition of the quotient rule is:

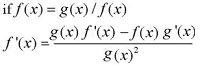
quotient rule definition

It looks ugly, but it’s nothing more complicated than following a few steps (which are exactly the same for each quotient). It can also be written a little more simply by getting rid of the formal function notation (e.g. by replacing f(x) with f):
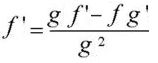
simplified quotient rule

You might also notice that the numerator in the quotient rule is the same as the product rule with one slight difference—the addition sign has been replaced with the subtraction sign.

Quotient Rule Examples

Watch the video for a step by step example:

Example Problem #1: Differentiate the following function:
f(x) = x3 + 2x2 – 1 / (x + 5)
Step 1: Choose f(x) and g(x).

  • The numerator (top function) is f(x): x3 + 2x2 – 1
  • The denominator (bottom function) is g(x): x + 5.

Step 2: Find f′(x) and g′(x) (the derivatives of f and g).

  • f′(x): 3x2 + 4x (I used the power rule)
  • g′(x): 1

Step 3: Plug your functions (from Step 1) and their derivatives (Step 2) into the quotient rule formula:

f&prime)(x) = (x + 5)( 3x2 + 4x) – ( x3 + 2x2 – 1)(1) / (x + 5)2

Step 4: Simplify (I used the Symbolab calculator):
f′(x) = 2x3 – 17x2 + 20x + 1 / x2 + 10x + 25

More examples for the Quotient Rule:

  1. (7x + 4)/(x2 + 5)
  2. How to Differentiate tan(x)

How to Differentiate (7x + 4)/(x2 + 5)

Step 1: Name the top term (the denominator) f(x) and the bottom term (the numerator) g(x).

  • f(x) = 7x + 4
  • g(x) = x2 + 5

Step 2:Find the derivatives of f and g:

  • f′(x) = 7
  • g′(x) = 2x

Step 3: Place your answers from Steps 1 & 2 into the quotient rule formula.
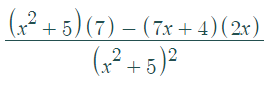
quotient rule formula example

Step 4:Use algebra to simplify where possible (I used Symbolab).
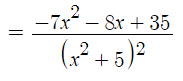
solution

How to Differentiate tan(x)

The quotient rule can be used to differentiate the tangent function tan(x), because of a basic identity, taken from trigonometry: tan(x) = sin(x) / cos(x).

Step 1: Name the top term f(x) and the bottom term g(x). Using our quotient trigonometric identity tan(x) = sinx(x) / cos(s), then:

  • f(x) = sin(x)
  • g(x) = cos(x)

Step 2: Find f′ and g′:

  • f′ = cos(x)
  • g′ = sin(x)

Step 3: Place your functions f(x) and g(x) into the quotient rule formula.

f′(x) = (cos x * cos x) – (sin x – sin x)/cos2x

Step 4: Use algebra to simplify . The solution is 1/cos2(x), which is equivalent in trigonometry to sec2(x).

Quotient Function

The term “quotient function” can refer to a few different things:

  1. Quotient Functions (a type of function in calculus)
    1. Definition,
    2. Domain,
    3. Quotient of Two Functions Example.
  2. The Quotient Function in Excel

1. Quotient Function (Type)

A. Definition

A quotient function is a type of function where two functions are separated by a division sign. For example:

  • f(x)/g(x)
  • X2/x
  • quotient function


B. Domain of a Quotient of Two Functions

The quotient of two functions, f(x) and g(x), has a domain A ∩ B (“A intersected with B” means the set of all points that A and B have in common), excluding where g(x) = 0.

The quotient is given by the following formula:
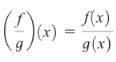
formula for quotient

Example question: If f(x) = √ (x + 1) and g(x) = 2x + 1:

  1. What is the quotient(q) of f and g?
  2. What is the domain of q?

Solution:
Part 1: Plug the given functions into the formula:
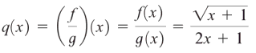
formula 2

Part 2: Find the domains for the two separate functions. As noted above, the denominator (in this case, 2x + 1) can’t equal zero. In other words, x ≠ -½.

The domain is all points that the two functions have in common.

  • The domain of f(x) = √(x + 1) is A = [-1, ∞). Why? Any number above -1 is fine, but -1 itself would give a denominator of 0. Any number lower than that, and you would be finding the square root of a negative number.
  • The domain of g(x) = B = (-∞, ∞).

The domain of the two functions overlap at [-1, ∞], so that’s the domain of this particular quotient function.

2. Quotient Function in Excel

The format for this function is:
QUOTIENT(numerator, denominator)

Note: A “function” in Excel refers to a predefined formula that performs calculations.

The quotient function in Excel is a bit of an oddity, because it only returns integers. For example, =QUOTIENT(7,2) gives a solution of 3 because QUOTIENT doesn’t give remainders. In other words, you should only use it if you want to discard a remainder. If you wanted to do a straightforward division (with remainder), just use the forward slash. For this example, type =7/3 into a cell instead.

References

Microsoft Office. Quotient Function. Retrieved October 19, 2019 from: https://support.office.com/en-us/article/quotient-function-9f7bf099-2a18-4282-8fa4-65290cc99dee
Tan S. (2008). Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach. Cengage Learning.
Wilson, R. (2013). Much Ado About Calculus: A Modern Treatment with Applications Prepared for Use with the Computer. Springer Science and Business Media. Retrieved OCtober 16, 2019 from: https://books.google.com/books?id=mqQACAAAQBAJ


Comments? Need to post a correction? Please Contact Us.