An auxiliary function isn’t a “real” function per se, it’s a placeholder. You usually create an auxiliary function to make calculations easier, or as a “stand in” function for a proof.
In addition to being placeholders in calculus equations. auxiliary functions play an important role in transcendental number theory. These functions are commonly used in various proofs and possess specific properties, such as frequently holding a value of zero or exhibiting a high-order zero at a particular point (Waldschmidt, 2008).
Auxiliary Functions in Integration
Auxiliary functions “u” and “v” come in handy when the expression you want to differentiate or integrate is complicated.
For example, let’s say you wanted to integrate the function
y = 2x(x2 + 3)70
The function is much easier to integrate if you use an auxiliary function “u” in place of x2 + 3:
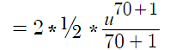
This particular use of “u” as an auxiliary function is called u substitution. A similar procedure is integration by parts (the UV rule), which uses a second auxiliary function “v” in addition to u.
Auxiliary Function in Proofs
When constructing a proof, sometimes you want to use an auxiliary function as a means to an end. In other words, inserting one into your proof may help you make a logical leap from “a” to “b”.
For example, the following proof of the mean value theorem (Chung, 2007). reaches a conclusion for an auxiliary function g so that Rolle’s theorem can be applied:
Let g: [a, b,] be the real-valued function
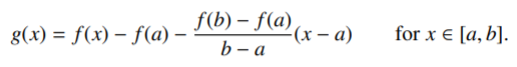
Where g is a continuous function on the closed interval [a, b] and differentiable on the open interval (a, b) with
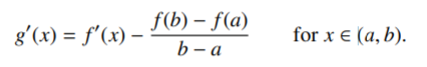
We have g(b) = g(a) = 0, so by Rolle’s Theorem, there exists a number (ξ) ∈ (a, b) such that g′(ξ) = 0, or equivalently:
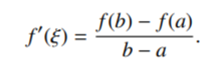
Note that I’ve introduced a proof here to demonstrate the idea of an auxiliary function. It isn’t intended to be a rigorous proof; If you do want a more comprehensive idea of the workings behind the proof, refer to S.K. Chung’s Basic Calculus, p.275
Auxiliary functions and the pigeonhole theory
Axel Thue and Carl Ludwig Siegel made a significant breakthrough in the 20th century regarding auxiliary functions. They realized that explicit knowledge of these functions is not always necessary. Instead, it suffices to understand their existence and certain properties. Using the Pigeonhole Principle, Thue — and later Siegel — proved the existence of auxiliary functions that exhibited specific characteristics, such as zeros at multiple points or high order zeros at a smaller set of points. Importantly, they showed that it was possible to construct such functions without excessive complexity. Rather than explicit functions, these auxiliary functions provided valuable insights and simplifications for transcendence proofs from the 19th century, leading to several novel results (Siegel, 1932).
Other mathematicians, including Alexander Gelfond (1934) and Theodor Schneider (also 1934), independently adopted and applied this method, ultimately proving the Gelfond-Schneider theorem. Alan Baker also utilized this method during the 1960s in his research on linear forms in logarithms, culminating in Baker’s theorem (Baker & Wüstholz, 2007). Baker’s theorem is a result in transcendental number theory that gives lower bounds for the absolute values of linear forms in logarithms.
References
Baker, Alan; Wüstholz, G. (2007), “Logarithmic forms and Diophantine geometry”, New Mathematical Monographs, Cambridge University Press, vol. 9, p. 198
Chung, S.K.(2007). Basic Calculus. Retrieved September 25, 2020 from: http://www.math.nagoya-u.ac.jp/~richard/teaching/f2016/BasicCalculus.pdf
Fischer, I. Basic Calculus Refresher. Retrieved September 25, 2020 from: http://pages.stat.wisc.edu/~ifischer/calculus.pdf
Gelfond, A. O. (1934). “Sur le septième Problème de D. Hilbert”. Izv. Akad. Nauk SSSR. 7: 623–630.
Siegel, Carl Ludwig (1932). “Über die Perioden elliptischer Funktionen”. Journal für die reine und angewandte Mathematik. 1932 (167): 62–69. doi:10.1515/crll.1932.167.62. S2CID 199545608.
Schneider, Theodor (1934). “Transzendenzuntersuchungen periodischer Funktionen. I. Transzendend von Potenzen”. J. Reine Angew. Math. 172: 65–69.
Waldschmidt, Michel. “An Introduction to Irrationality and Transcendence Methods” (PDF).