Types of Functions > Superadditive function, subadditive
Contents (Click to skip to that section):
- What is an Additive Function?
- Completely (Totally) Additive Function
- Subadditive function
- Superadditive Function
1. Additive Function Definition
One of the simplest types of arithmetical functions is the additive function, which has the form
f(ab) = f(a) + f(b)
for all relatively prime (coprime) positive integers a and b. Relatively prime means that two integers don’t share any common factors except 1. For example, 6 and 5 are relatively prime, as are 30 and 7.
This type of function has some interesting properties. For example, we can easily prove that if a real valued function f(x) is bounded and additive, the function is equal to zero for all x.
Examples of Additive Functions
If a and b are relatively prime positive integers, then the logarithm
log(ab) = log(a) + log(b)
is an additive function.
It doesn’t matter what base your log is in. For example:
- log(10) = log(5) + log(2),
- ln(6) = ln(3) + ln (2).
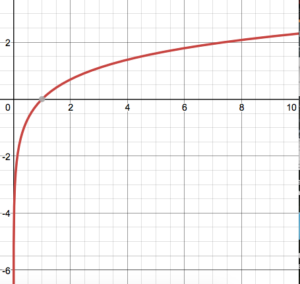
The image below shows the graph of ln(x) between 0 and 10. It is an additive function because for all positive, coprime a and b, ln(ab) = ln(a) + ln(b).
Another additive function is ω (n), the function which returns the number of distinct prime factors of any number. You can test this yourself by trying some coprime values—5 and 12, for example.
Since 5 is a prime number, it has just one distinct prime factor—itself! So >ω(5) = 1.
To find the number of prime factors of 12, we draw a prime factor tree.
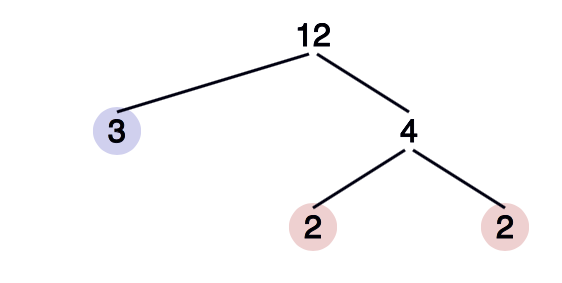
So, ω(12) = 2.
In summation:
- ω(5) = 1
- ω(12) = 2.
And if ω is an additive function, ω(60) = ω(5) + ω(12) = 3. We test this by making another prime factor tree

And find out we were right; 60 has just three distinct prime factors, 5, 3, and 2!
Ω (n), the function which returns the number of nondistinct prime factors, is also additive.
2. Completely (Totally) Additive Function
If the function f(ab) = f(a) + f(b) holds even when a and b are not relatively prime, f(x) is completely additive (also called totally additive). For every function f that is completely additive, f(1) = 0.
Subadditive Function
A subadditive function is formally defined as one where the following inequality holds (Kadakal, 2020):
f (x + y) ≤ f(x) + f(y),
for x, y ∈ [0, ∞).
Superadditive Function
A superadditive function can be defined in terms of a subadditive function. A function is superadditive on an interval if and only if –f is subadditive. To put this in notation, a function is superadditive on an interval if the following inequality holds:
f (x + y) ≥ f(x) + f(y)
Note that the inequality is reversed: some definitions of superadditive simply state that if the inequality in the definition of a subadditive function is reversed, then that function is superadditive.
What those definitions are saying, in general terms, is that if you evaluate a subadditive function for the sum of any two elements in the domain, you’ll always get something less than or equal to the sum of the function values at each element. The reverse is true for the superadditive function: you’ll always get something more (or equal to) the sum of the function values.
Superadditive and subadditive functions are important in the study of differential equations, convex bodies, inequalities, number theory and semi-groups.
Examples of Superadditive Function
Every additive function is subadditive and superadditive.
For example, logb (x) is an additive function, because logb(x, y) = logb x + logb y.
A star-shaped function, with respect to the origin, is superadditive. Another example is a convex function f with f(0) ≥ 0 (Bruckner, 1962). Note though, that a superadditive function isn’t always convex, even with (0) = 0.
References
Brucker, A. (1962). Tests for the Superadditivity of Functions. Pacific J. Math. 10 (1960), no. 4, 1155–1162.
Kadakal, H. (2020). Hermite-Hadamard type inequalities for subadditive functions. AIMS Mathematics, 5(2): 930–939.
Nathanson, M. Additive Number Theory: Inverse Problems and the Geometry of Sumsets (Graduate Texts in Mathematics) (Vol 165) 1996.