There’s a lot of confusion about the correct definition of an Into Function.
It is sometimes defined as a function that [1]
…maps X into Y if and only if for each x in X, f(x) is in Y.
Or a function “…for which the range is a subset of the codomain” [2]. This seems to agree with the first definition. A quick Google search brings up this more formal definition [3], which also seems to be in agreement:
A function f is into Y iff the range of f is a subset of Y . i.e., Rf⊂Y.
However, other authors define an into function a little differently. For example, Kumar [4] sets the requirement that there must be at least one element in a set B which is not mapped by any element of set A. Cue Math [5] agrees with this definition:
“…for an into function, there should be at least one element in the output set B that should not be connected to the elements of the input set A.”
So, What’s the Correct Definition for an “Into Function”?
Perhaps the biggest clue in solving the puzzle is that entries for “Into function” are notably absent from Wolfram Mathworld and even Wikipedia.
So, why is that? It seems to indicate that a formal definition for Into Function does not exist.
That means there probably isn’t a “correct” definition at all. One thing is for sure, an into function is not a synonym for injective, as this post on Stack Exchange points out. The confusion may come from the fact that surjective functions are sometimes described as being “onto”. However, it doesn’t mean that an injective function is “into.”
This is one of those definitions that you have to take with a grain of salt. Treat it as a loose definition or a colloquialism. If a website is talking about an Into Function in the same breath as an Onto Function, then they are most likely (incorrectly) referring to an injective function. But if you are reading a good book on set theory, they are probably (but not always) using the definition pointed out in the Stack Exchange article (which cites [6]), which is
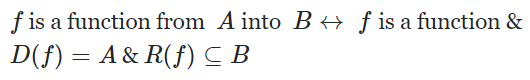
References
[1] Rodgers, N. (2011). Learning to Reason. An Introduction to Logic, Sets, and Relations. Wiley.
[2] Dybkær, R. (1968). APMIS Supplementum. Munksgaard.
[3] Tiwari, G. Set Theory, Functions and Real Numbers. Retrieved March 7, 2022 from: https://gauravtiwari.org/set-theory-functions-and-real-number-system/#into-function
[4] Kumar, (201). Theory of Automata. McGraw-Hill Education (India) Pvt Limited Language: English.
[5] Cue Math. Retrieved March 7, 2022 from https://www.cuemath.com/algebra/onto-function/
[6] Suppes, P. (1960). Axiomatic Set Theory. Dover.