Beta Function, Incomplete Beta: Simple Definition, Examples

Types of Functions > Beta Function, Incomplete Beta

Contents:

1. Beta Function
2. Incomplete Beta Function
3. Regularized incomplete beta function

Beta Function

The Beta function (also called the Euler Integral of the first kind) is a definite integral, related to the gamma function. The most common representation for the function is:
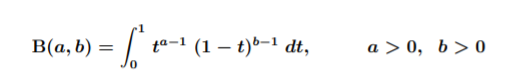
The function goes by many different names. As is is usually defined by the above integral, it is sometimes called the “beta integral.” It’s also called the Euler Β-function, and is sometimes simply denoted by its variables: Β(p, q).

Other equivalent forms of the function exist, and are obtained by changing variables. You can find a list of various forms (including trigonometric forms) in the Digital Library of Mathematical Functions.

Practical Uses

The Beta function has practical applications in physics, string theory, and time management:

• In physics, it can model properties of the strong nuclear force. It is also used to describe the scattering amplitude of Regge trajectories. These trajectories are curves that link a particle’s energy, momentum, and spin. The beta function also serves as the initial known scattering amplitude in string theory.
• In time management, the beta distribution, which is the integrand of the Beta function, is used to estimate the average time to complete tasks.
• In calculus, the Beta function can simplify the evaluation of many complex integrals by rewriting them as Beta functions.

In probability and statistics, the Beta function has various applications. For example, it can be used to calculate confidence intervals in various statistical estimations. it can also be used to calculate the probability a random variable will fall within a specific range. For example, suppose that a random variable follows a beta distribution with parameters α and β. The probability that a random variable will take on a value between x and y is given by

Probability = (Beta function of (x + 1, β + 1)) / (Beta function of (α + 1, β + 1))

where

• x and y are the lower and upper range bounds
• α and β are the beta distribution’s parameters.

The beta function has applications as a normalizing constant and is part of the definitions of many probability distributions. For example, the probability mass function (PMF)for the Yule-Simon distribution incorporates the beta function. The function can also define a binomial coefficient after adjusting indices. These statistical applications extend to real-life scenarios such as modeling experimental frequency distributions of relative sunshine and humidity.

History

While Euler first developed the function, it was the French mathematician Jacques P.M. Binet who first used the beta symbol for the function.

Incomplete Beta Function

The incomplete beta function (also called the Euler Integral) is a generalized β-function; An independent integral (with integral bounds from 0 to x) replaces the definite integral. The formula is:
Where:

• 0 ≤ x ≤ 1,
• a, b > 0. Note: The definition is sometimes written to include negative integers (e.g. [1]) but this isn’t commonplace.

B₁(p, q) is the (complete) beta function; in other words, the function becomes complete as x = 1. The incomplete beta function can also be expressed in terms of the beta function or three complete gamma functions [2].

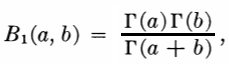
Incomplete Beta-Function Ratio

The ratio of
to
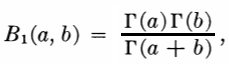
is called the incomplete beta function ratio. Represented by the symbol I_x, it is written as: I_x (a, b) ≡ B_x(a, b) / B₁(a, b). Where a > 0, b > 0 [3].

Incomplete Beta Function Uses

The incomplete beta function and I_x crop up in various scientific applications, including atomic physics, fluid dynamics, lattice theory (the study of lattices) and transmission theory [4]:

• Calculating confidence intervals for t-tests, F-tests [5] and those based on the binomial distribution, where the incomplete beta function is used to calculate the limits [6],
• Computing the probability in a binomial distribution tail [7] or binomial limits [6],
• Creating cumulative probabilities for the standard normal distribution [8].
• Finding a measurement larger than a certain value, for data following a beta distribution.

Regularized incomplete beta function

The regularized incomplete beta function, also known as the regularized beta function, is often used in statistics and physics. It is as the cumulative distribution function (CDF) of the beta distribution [9], representing the CDF for a random number Y that follows the beta distribution [10].

The regularized incomplete beta is used when calculating the incomplete beta independently is inconvenient. The “regularized” version divides this function by the complete beta [11], which gives rise to an alternate name – the incomplete beta function ratio [12].

The regularized incomplete beta is defined in terms of two functions: the incomplete beta B(z; a, b) (the Euler integral), and the complete beta b(a, b) [13]:

This definition cannot be used for nonpositive integers a or b, as it would result in an indeterminate expression. In such cases, a more comprehensive definition, may be required. For example [14]:

References

1. Özçag, E et al. (2008). An extension of the incomplete beta function for negative integers, J. Math. Anal. Appl.
2. DiDonato, A. & Jarnagin, M. (1972). A Method for Computing the Incomplete Beta Function Ratio. U.S. Naval Weapons Laboratory. Retrieved September 21, 2020 from: https://apps.dtic.mil/dtic/tr/fulltext/u2/642495.pdf
3. DiDonato, A. & Jarnagin, M. (n.d.). The Efficient Calculation of the Incomplete Beta-Function Ratio for Half-Integer Values of the Parameters a, b. Retrieved September 21, 2020 from: https://www.ams.org/journals/mcom/1967-21-100/S0025-5718-1967-0221730-X/S0025-5718-1967-0221730-X.pdf
4. DiDonato, A. & Morris, F. (1988). Significant Digit Computation of the IBF. Retrieved September 21, 2020 from: https://apps.dtic.mil/dtic/tr/fulltext/u2/a210118.pdf (PDF).
5. Besset, D. (2001). Object-Oriented Implementation of Numerical Methods. An Introduction with Java & Smalltalk. Elsevier Science.
6. Young, L. et al. (1998). Statistical Ecology. Springer. [6] Young, L. et al. (1998). Statistical Ecology. Springer. [Google books]
7. DTIC–Defense Technical Information Center (1979). A Note on the Incomplete Beta Function. Klugman, S. et al. (2013). Loss Models. Wiley.
8. Klugman, S. et al. (2013). Loss Models. From data to decisions. Wiley.
9. Conte, E. On a Simple Derivation of the Effect of Repeated Measurements on Quantum Unstable Systems by Using the Regularized Incomplete Beta. Adv. Studies Theor. Phys., Vol. 6, 2012, no. 25, 1207 – 1213.
10. Nordén, B. et al. (Eds.). (2020). Entropy-Enthalpy Compensation. Finding a Methodological Common Denominator Through Probability, Statistics, and Physics. Jenny Stanford Publishing.
11. Wolfram, S. (2003). The Mathematica Book Volume 1. Wolfram Media.
12. Muller-Bungart, M. (2007). Revenue Management with Flexible Products. Models and Methods for the Broadcasting Industry. Springer.
13. Weisstein, E. (1999). Regularized Beta. Retrieved July 15, 2023 from: https://archive.lib.msu.edu/crcmath/math/math/r/r199.htm [14] Wolfram. BetaRegularized. Retrieved June 18, 2022 from: https://functions.wolfram.com/GammaBetaErf/BetaRegularized/02/01