Many different types of correlation function exist. Their exact definitions depend on what field you’re working in. For example:
- In statistics, a correlation function can find the correlation of two random variables or systems. “Correlation” is a measure of how one value or system responds to another.
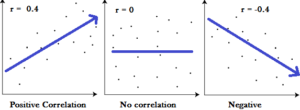
A correlation function can show how systems are correlated.
The strength of correlation depends on the spatial or temporal distance between the random variables. - Also in statistics, the Auto Correlation Function (also called a correlogram) shows serial correlation in data (where error terms transfer from one period to another) that change over time.
- In statistical mechanics, a mathematical correlation function measures order in a system and describes spatial correlation—how microscopic variables, like density or spin, are related at different positions. For example, the function is often used to describe how spins of ferro- and antiferromagnetic materials align with respect to their nearest neighbors. One application in physics assesses the probability of finding a particle’s center relative to another particle’s center [1]. This can be extended to galaxies, as a measure of the excess probability of finding a galaxy at a certain distance from another galaxy, compared to what you would expect with a random distribution of galaxies. See [2] for a slightly different definition and more details on cosmology applications.
Time Correlation Function
Time correlation functions, or time-dependent correlation functions, are used in the theory of noise and stochastic processes including statistical physics and spectroscopy. They are a measure of the correlation of two dynamical properties over time. Mathematically, the correlation function is defined as [3]:
Cαβ(t) = <α(0)β(t)>
The brackets <> indicate an average for the equilibrium ensemble.
If the two properties αβ are the same, the correlation function is called an autocorrelation function. If they are different, it’s a cross-correlation function.
Time-correlation functions are also used in quantum mechanics, where they represent the dynamics of a system. They give a statistical description of an ensemble variable’s time-evolution of at thermal equilibrium. These functions are often used to model both random and stochastic irreversible processes in condensed phases [4].
References
[1] Croker, J. & Weeks, E. What is the Pair Correlation Function? Retrieved April 4, 2021 from: http://www.physics.emory.edu/faculty/weeks//idl/gofr.html
[2] B. The correlation function: galaxies. Retrieved April 4, 2021 from: https://ned.ipac.caltech.edu/level5/March04/Jones/Jones5_2.html
[3] Berne, B. & Harp, G. (1970). On the Calculation of Time Correlation Functions. Advance in Chemical Physics, Volume XVII.
[4] MIT Open Courseware. (2009). 5.74 Introductory Quantum Mechanics II. Retrieved April 4, 2021 from: https://ocw.mit.edu/courses/chemistry/5-74-introductory-quantum-mechanics-ii-spring-2009/lecture-notes/MIT5_74s09_lec05.pdf CC Sharealike 4.0.