Contents:
What is a Quartic Function?
A quartic function is a fourth-degree polynomial: a function which has, as its highest order term, a variable raised to the fourth power.
It can be written as:
f(x) = a4 x4 + a3 x3 + a2 x2 +a1 x + a0.
Where:
- a4 is a nonzero constant.
- a3, a2, a1 and a0 are also constants, but they may be equal to zero.
The derivative of every quartic function is a cubic function (a function of the third degree).
The quartic was first solved by mathematician Lodovico Ferrari in 1540.
Watch the video for an overview of quartic functions, or read on below:
Graph of a Quartic Function
The graph of a fourth-degree polynomial will often look roughly like an M or a W, depending on whether the highest order term is positive or negative.
- If the coefficient of the leading term, a, is positive, the function will go to infinity at both sides.
- If the coefficient a is negative the function will go to minus infinity on both sides.
The term a0 tells us the y-intercept of the function; the place where the function crosses the y-axis. The roots of the function tell us the x-intercepts.
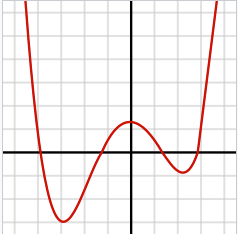
The image below shows the graph of one quartic function. This particular function has a positive leading term, and four real roots.
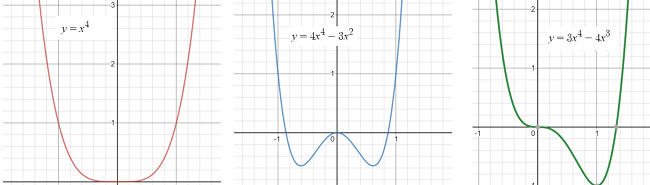
Three basic shapes are possible. For a > 0:
Properties of Quartic Polynomials
Fourth degree polynomials all share a number of properties:
- They have up to four roots,
- Their derivatives have from 1 to 3 roots,
- They have no general symmetry,
- They can have one, two, or no (zero) inflection points,
- Five points, or five pieces of information, can describe it completely,
- Every polynomial equation can be solved by radicals.
Quartic Curve Examples
A quartic curve is any curve given by a fourth degree polynomial. It can be defined by the following equation
Ax4 + By4 + Cx3y + Dx2y2 + Exy3 + Fx3 + Gy3 + Hx2y + Ixy2 + Jx2 + Ky2 + Lxy + Mx + Ny + P = 0.
Examples of quartic curves:
References
Davidson, Jon. Fourth Degree Polynomials. Retrieved from https://www.sscc.edu/home/jdavidso/math/catalog/polynomials/fourth/fourth.html on May 16, 2019.