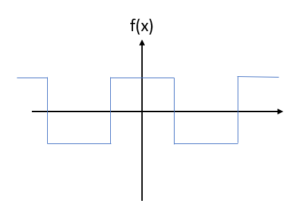
A square wave function (also called a pulse wave or Rademacher function) is a periodic function that constantly pulses between two values. Common values include the digital signal (0, 1), (-1, 1) and (-½, ½). It is also an odd function, which means it is symmetric around the origin.
In function notation, the square wave function is represented as follows (for a pulse between 1 and -1, pulsing around π):
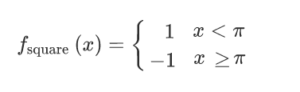
Relationship to the Boxcar Function
The square wave function can also be thought of as a periodic expansion of the boxcar function. The graph of a boxcar function has the shape of a boxcar sitting on a “railway track” (the x axis); A periodic expansion would have boxcars placed at constant intervals on the x-axis— creating the square wave function. This may be why this periodic expansion is sometimes called a pulse train.
Approximations
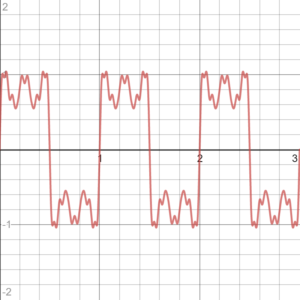
The sine function and cosine function can be used to approximate a square wave function. As an example, the following graph is the sine function f(x) = sin 2πx + (1/3) sin 3 (2πx) + (1/5) sin 5 (2πx) + (1/7) sin 7 (2πx) + (1/9) sin 9 (2πx) + (1/11) sin 11 (2πx) + (1/13) sin 13 (2πx) + (1/15) sin 15 (2πx) + (1/17) sin 17 (2πx) + (1/19) sin 19 (2πx):
Real Life Uses of the Square Wave Function
Square wave functions are often used in computer science and electrical engineering. For example, it’s used in engineering to model forces acting on a mechanical system or in an electric circuit.
References
Braithwaite, C. (2014). General Inner Product & Fourier Series. Advanced Topics in Linear Algebra, Spring.
Desmos.com (graph)Dobrushkin, V. MATHEMATICA TUTORIAL for the Second Course. Part V: Square wave functions
. Retrieved December 12, 2019 from: http://www.cfm.brown.edu/people/dobrush/am34/Mathematica/ch5/step.html
Singh, M. Fourier Series.