The probit function Φ(x) is the inverse of the standard normal cumulative distribution function. It maps a value for probability p onto the real number line for values of p between 0 ≤ p ≤ 1. The name “probit” is a contraction of “probability unit” [2].
The probit function of a probability p gives the z-score associated with p a standard normal distribution. For example, probit(0.5) = 0 and probit(1.96) = .975. In other words, z-values of 0 and 1.96 correspond to the cumulative areas of 0.5(50%) and .975(97.5%) respectively for a standard normal distribution. Essentially, when you find “inv norm” in a statistical package, you’re finding values for the probit function.
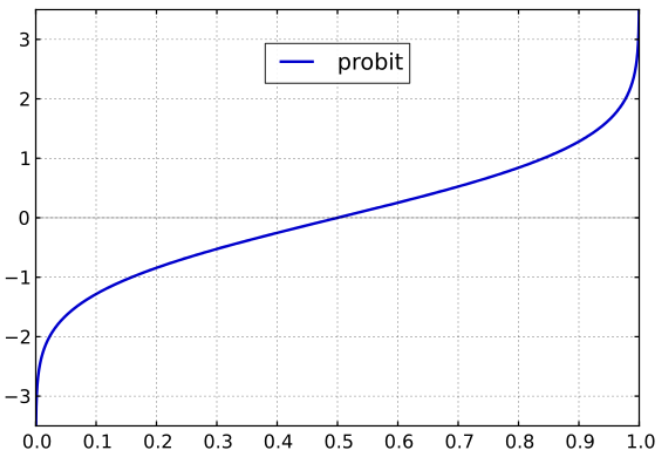
The domain of the probit function is from 0 to 1. The range is from -∞ to ∞.
The graph is sigmoidal in shape:
Formal Definition
The probit is a monotonically increasing function defined by the error function of a normal distribution [1]:
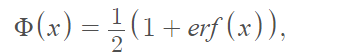
Where
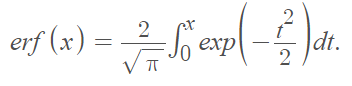
Probit Function Use
The function has many uses in statistical modeling; the generalized linear model based on the probit function is called probit regression.
The probit function was first proposed in 1934 in connection with the percentage of a pest killed by a certain pesticide [3]. Since then, it has found a wide variety of uses in medicine, toxicology, and related fields where risk of exposure to a substance is measured. For example:
- The probit function can be used to describe the relationship between the period of exposure to a toxic chemical, chemical concentrations in air, and response rate [4].
- The fatality rate of personnel exposed to hazardous agents for a given time period can also be calculated by use of probit functions [5].
References
Probit function graph: Geek3,
[1] Jiang, H. (2021). Machine Learning Fundamentals: A Concise Introduction. Cambridge University Press.
[2] Bliss, C. (1934). The Method of Probits. 12;79(2037):38-9. doi: 10.1126/science.79.2037.38.
[3] Bliss, C. I. (1934). “The method of probits“. Science. 79 (2037): 38–39.
[4] Bergström, U. et al. (2019). Probit functions for selected chemicals based on AEGL3 values. Retrieved April 13, 2022 from: https://www.foi.se/rest-api/report/FOI-R–4720–SE
[5] HSE. Methods of approximation and determination of human vulnerability for offshore major accident hazard assessment.