Contents:
Radicals and Square Roots
Algebraically, a square root is usually shown as √(a2) = a where “√” is called the radical sign. Square roots can also be represented, equivalently, as x½ or 2√a.
A square root contains a radical symbol, but square roots and radicals aren’t the same thing. A square root is a radical with a power of 2. Other radicals include:
- Power of 3 (cubic),
- Power of 3 (quartic),
- Power of 3 (quintic).
What is a Radical Function?
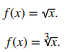
Example of a Radical Function
Perhaps the simplest example of a radical function is the square root function. It is the inverse of the power function. The curve looks like half of the curve of the parabola y = x 2, with x and y reversed.
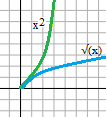
Since the inside of the square root must be positive, the domain of this function is (0, ∞).
We can graph more complicated square root functions by beginning with this basic graph and then reflecting or translating the graph as appropriate. The graph of
![]()
for example, is the square root graph shifted two units to the right. The domain of this graph is [2, ∞).
Finding the Domain of a Radical Function
Watch the video for a couple of examples of how to find the domain and range for a square root function, or read on below for other radical functions:
To find the domain of this type of function, remember that even powers of any number— negative or positive— are always positive. That means that the expression inside an even radical must always be positive, too.
Start by finding the index of the radical. An index number is just the little number to the left of the radical sign. It tells us which root we are taking: the fourth root, the fifth root, or whatever it might be. If there’s no little number to the left of the square root sign, that means the index is just two.
The important thing here is that indexes can be odd or even.
- An odd index means the domain of the function is all real numbers.
- An even index means the expression inside the radical must be greater than or equal to zero. If the expression inside the radical is just x, the domain is (0, ∞), as for the square root function above.
References
College of the Redwoods. Intermediate Algebra Textbook, Chapter 9. Retrieved from http://msenux2.redwoods.edu/IntAlgText/chapter9/chapter9.pdf on July 5, 2019.
Pike, Scott. Mat 120/121/122 Course Notes. Finding the Domain of a R Function. Retrieved from http://www.mesacc.edu/~scotz47781/mat120/notes/radicals/domain/any_index/any_radical.html on July 5, 2019