< Statistics definitions < Bivariate Correlation and Regression
What is Bivariate Correlation?
Bivariate correlation analyzes the relationship between two variables — usually two types of related data such as caloric intake and weight, income and house expenditures, or daily temperature and ice cream sales [1]. It tests whether the two variables have a linear relationship, meaning that one variable changes in a linear way as the value of the other variable changes. Generally, bivariate correlation describes the effect of two or more phenomena occurring together.
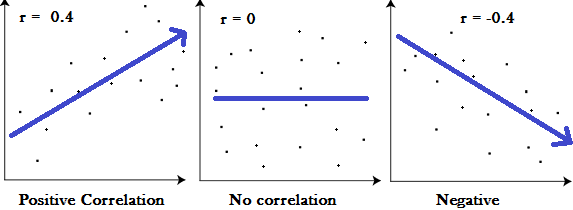
The most common way to quantify bivariate correlation is with Pearson’s r, also called the Pearson product-moment correlation coefficient (PPMCC). Pearson’s r measures the linear relationship between two variables. It ranges from -1 to 1, where a correlation of 1 indicates perfect positive correlation, a correlation of -1 indicates perfect negative correlation, and a correlation of 0 indicates no correlation [2].
PPMCC is calculated by taking the covariance of the two variables and dividing it by the product of their standard deviations. Covariance measures how two variables change together, while standard deviation measure’s a variable’s spread [3].
Bivariate correlation can be visualized using a scatterplot, which is a graph with two axes, one for each variable. Each data point on the scatterplot represents a pair of values for the two variables [4].
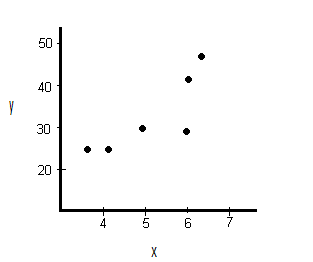
When correlation is high, the data points will be clustered together in a narrow band. When the correlation is low, the data points will be more spread out. The above image shows a simple scatterplot with medium correlation; that is, the points appear to cluster around a line, although the fit is far from perfect.
Bivariate correlation vs bivariate regression
Bivariate correlation and bivariate regression both analyze the relationship between two variables. However, they serve different purposes. While bivariate correlation measures the strength and direction of the linear relationship between two variables, bivariate regression predicts the value of one variable (the dependent variable) based on the value of another variable (the independent variable). It is calculated by fitting a linear model to the data then using that model to predict values.
Suppose we are interested in the relationship between height and weight. We could use bivariate correlation to measure the strength and direction of the linear relationship between height and weight. If the correlation is significant, then this would indicate that there is a linear relationship between the two variables, meaning that taller people tend to be heavier and shorter people tend to be lighter.
However, if we want to predict the weight of a person based on their height, then we would need to use bivariate regression. We would fit a linear model to the data and then use that model to predict the weight of a person for a given height. Bivariate regression model is simply a special case of regression that involves only two predictors [5].
Bivariate data can be analyzed with many different types of bivariate regression, depending on whether data is discrete or continuous [6]:
| Independent variable | Dependent Variable | Regression type |
| Continuous | Continuous | Ordinary Least Squares |
| Continuous | Discrete | Logistic regression |
| Discrete | Continuous | T-Test, ANOVA |
| Discrete | discrete | Categorical data analysis |
References
[1] Math is Fun. Definition of Bivariate Data.
[2] SPSS Tutorials: Pearson Correlation. Retrieved October 12, 2023 from: https://libguides.library.kent.edu/spss/pearsoncorr
[3] Sam, P. Standard Deviation. Retrieved October 12, 2023 from: https://probabilityhowto.com/standard-deviation/
[4] PEP 6305 Measurement in Health & Physical Education. Topic 6: Correlation. Retrieved October 12, 2023 from: https://grants.hhp.uh.edu/doconnor/pep6305/topic%20006%20correlation.htm
[5] Bivariate Linear Regression. Retrieved October 12, 2023 from: https://jbusemey.pages.iu.edu/lect6/lect6_p553.pdf
[6] Bivariate regression. Retrieved October 12, 2023 from: https://www3.nd.edu/~rwilliam/stats1/x71.pdf