What is the Popcorn Function?
The Popcorn function is named because of its resemblance to popping corn:
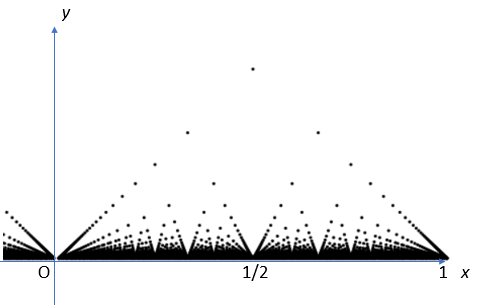
The formula is:
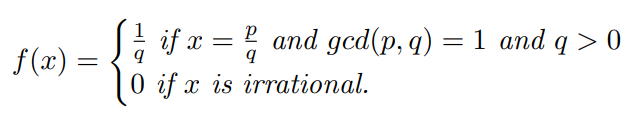
Different authors define the function in slightly different ways. For example, coprimes might be used instead of greatest common divisor (gcd). This is not a big difference, because coprime integers are equivalent to their greatest common divisor (gcd) of 1. The hallmark characteristic of the function though is that it is discontinuous at rational points and continuous at irrational points.
A Modification of the Dirichlet
The function is a modified version of the Dirichlet function: usually defined as 1 for rational numbers (i.e. those numbers that can be written as a ratio, like 3/4 or 10/5) and 0 elsewhere.
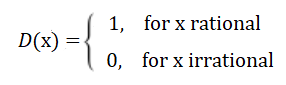
The modification solves the problem of the dense graph the Dirichlet produces. The points (popcorn kernels, if you will) are so tightly packed together that the graph of the Dirichlet looks like a straight line:
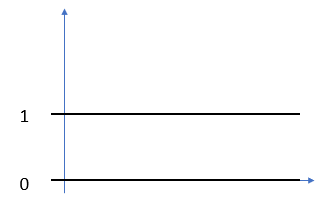
However, it is actually a series of points, so tightly packed together they are indistinguishable.
The popcorn function takes these points and distributes them so that they are more easily seen.
Properties of the Popcorn Function
The Popcorn function does exhibit some very unusual behavior. A few properties of the function will show how this strange behavior works:
- The limit at every point a is zero (quite normal behavior, so far),
- The function is continuous at points with a value of 0. This means that it is
- A continuous function for all irrational numbers,
- A discontinuous function for all rational numbers.
Here’s where things get strange: the function is discontinuous for all rational numbers, which results in problems with interpreting and working with the function. However, the limit there is zero. That means those points are removable discontinuities, which makes the popcorn function (weirdly) a continuous function, even though it isn’t intuitively so.
Other Names
The Popcorn Function goes by many other names, including the Countable Cloud function, Raindrop function, Ruler function, also:
- Dirichlet function (Bruckner et al. 2008),
- Riemann function (Yurij 2017, p.89)
- Small Riemann function (Ballone 2010, p. 11),
- Thomae function (Beanland et al. 2009),
Confusingly, other functions take on the name “popcorn function.” For example, Pole (2011) defines it as a type of sine function:
yt = I sin (t)
Where I is an indicator function.
The takeaway: make sure you know which specific function the author is referring to.
References
Dirichlet function and its modifications. Retrieved January 29, 2020 from: http://math.feld.cvut.cz/mt/txtb/4/txe3ba4s.htm
Ballone, F.(2010). On Volterra Spaces. Masters thesis, Youngstown State University.
Beanland, K. et al. (2009). Modifications of Thomae’s Function and Differentiability. Amer. Math. Monthly 116, 531-535.
Bruckner, A. et al. (2008). Elementary Real Analysis, 2nd ed.. Upper Saddle River, NJ: Prentice Hall.
Dixon, R. (1991) Mathographics. New York: Dover, pp. 177 and 184-186.
Kane, J. (2016). Writing Proofs in Analysis. Springer.
Morrow, J. (2010). Thomae’s Function. Retrieved January 29, 2020 from: https://sites.math.washington.edu/~morrow/334_15/thomae.pdf
Pole, A. (2011). Statistical Arbitrage: Algorithmic Trading Insights and Techniques. John Wiley & Sons.
Trott, M. (2004). The Mathematica GuideBook for Programming. New York: Springer-Verlag, pp. 32-33. http://www.mathematicaguidebooks.org/.
Yurij, H. (2017). Order, Disorder And Criticality – Advanced Problems Of Phase Transition Theory -, Volume 5. World Scientific.