For many continuous random variables, we can define a probability density function (PDF) to find probabilities of the variable falling within a range, say a and b. This probability is denoted by P (a < X < b) and is more formally given by [1]:
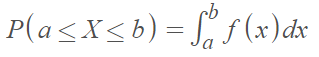
The probability that X is on the closed interval [a, b] can be calculated by integrating the pdf of the random variable X.
A continuous random variable (like one describing height, temperature, or weight) has possible values of either:
- One interval on the number line, or
- A union of disjoint intervals (“disjoint” means no points in common).
For example, let’s say an oceanographic study was taking depth measurements at random locations in the Pacific. The range for X, a continuous random variable, is the minimum possible depth (0 feet) to the maximum possible depth (36,161 feet). If we were also taking measurements in the Dead Sea (1,412 ft to 2409 ft below sea level), we would have a union of two disjoint intervals.
In some applications, the term probability distribution function is synonymous with probability density function.
PDF, CDF and the FTC
The PDF of a continuous random variable is also the derivative of its CDF. The Fundamental Theorem of Calculus allows us to express the CDF, F(x), in terms of its PDF [2]:
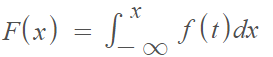
Probability Density Function vs. Probability Mass Function
If the random variable can only have certain values (like drawing cards from a standard deck), a probability mass function (PMF) describes the probabilities of the outcomes. On the other hand, continuous random variables are not restricted to a set of certain values: they can take on any number within a range (like a number with 10,000 decimal places). If you have continuous variables, you can’t write out every possible value because you would have infinite possibilities to write out (which is, of course, impossible).
In fact, because there are infinite possibilities, the probability that a continuous random variable takes on any specific value of x is zero (because 1/∞ = 0). In other words, it is not possible to calculate P(X = x) for a continuous random variable; What you can do is create a formula; The formula that describes all possible outputs.
PDF Properties
For f(x) to be a “legitimate” pdf, it must have the following properties:
- f(x) ≥ 0 for all x (in other words, f(x) must be nonnegative for every value of the random variable).

Probability Density Function Examples
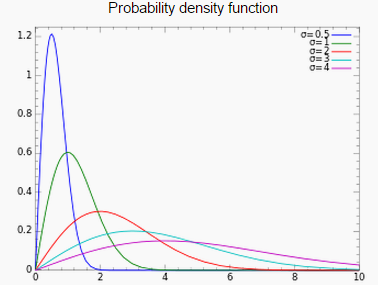
Rayleigh Distribution PDF
The notation X Rayleigh(σ) means that the random variable X has a Rayleigh distribution with shape parameter σ. The PDF (X > 0) is:
![]()
Where e is Euler’s number.
The distribution gets wider and flatter as σ increases.
Normal Distribution
The normal distribution (a.k.a. the “bell curve”) is defined by the PDF:
![]()
Where:
- μ and σ are fixed constants.
- ex = Exponential function [3].
References
[1] Continuous Random Variables and Probability Distributions. Retrieved August 1, 2021 from: https://www.colorado.edu/amath/sites/default/files/attached-files/ch4_0.pdf
[2] 2.3 – The Probability Density Function. Retrieved August 1, 2021 from: https://blogs.ubc.ca/math105/continuous-random-variables/the-pdf/
[3] Kjos-Hanssen, B. (2019) Statistics for Calculus Students. Retrieved April 30, 2021 from: https://dspace.lib.hawaii.edu/handle/10790/4572
