The hyperbolic sine function, first studied by the 18th century mathematician Jacopo Riccati, is an odd function defined as half of the difference between the exponential functions ex and e-x:
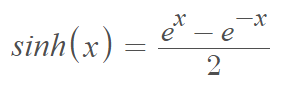
The function defines the hyperbolic sine of an angle. It’s similar to how a sine works for a unit circle, except here we’re working with a hyperbola instead of the unit circle.
The domain and range include real (-∞, ∞) and complex values. For a complex argument, the identity is
sinh(x) = −isin(ix).
All hyperbolic functions can be written as a series, and the hyperbolic sine function is no exception. It can be written as:

The denominators rapidly increase, which means that higher order terms soon become insignificant. This results in the approximation
sinh(x) ≈ x, x → 0.
Derivative and Integrals
The derivative of the hyperbolic sine is the hyperbolic cosine function, cosh(x).
Taking the derivative and setting it equal to zero usually gives us a function’s critical points. However, ex is always positive, which means the derivative of sinh x is never zero. Therefore, the hyperbolic sine doesn’t have any critical points.
Taking the second derivative and setting it equal to zero gives us the inflection point(s). The second derivative is sinh(x), which equals 0 when ex = e-x, or when x = 0. Therefore, the hyperbolic sine has one inflection point, at x = 0.
The integral of sinh(x) is coshx + C.
Graph of the Hyperbolic Sine Function
The graph of the hyperbolic sine function is shown below:
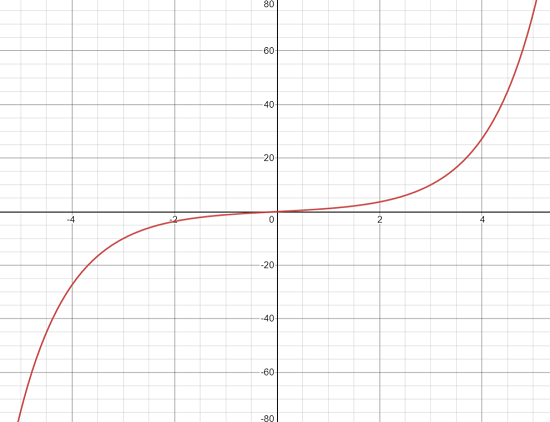
It is a monotonic function, unlike its trigonometric relative the sine function, which is a periodic function.
Identities
The hyperbolic sine has many useful identities, including:
- sinh(-x) = -sinh (x)
- sinh (x + y) = sinh (x) cosh(y) + cosh(x) sinh(y)
- sinh(x) + cosh(x) = ex
- sinh(x) – cosh(x) = -ex
- cosh2(x) – sinh2(x) = 1
References
Graph created with Desmos.com.