What is an Identical Function?
An identical function has a matching “twin” function. Their graphs overlap completely.
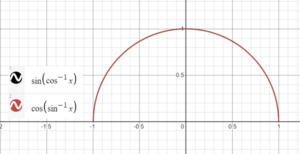
More formally, two functions are identical (or equal) if
- Both functions have equal domains,
- Both functions have equal ranges,
- The functions are equal for all values in the domain.
Although two identical functions always have overlapping graphs, the converse isn’t always true; You can’t simply graph two functions are conclude they are identical because their graphs overlap. It is possible for two functions to look the same on a graph, yet not meet the stringent requirements for an identical function. As an example, the graphs of x3/x, x4/x2 and x 2 overlap:
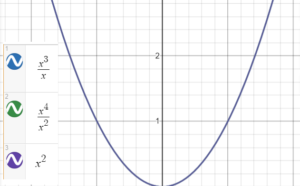
However, they are not identical because they do not have the same domains:
- x3/x and x4/x2 have domains of the set of non-zero real numbers,
- x 2 has a domain of the set of real numbers.
In other words, you’ll find a hole at zero of the first two functions that doesn’t exist on the third. This is practically impossible to see on a standard graph, which is why it’s so important to compare domains and ranges.
Identical Function in R
In R, the identical(x, y) function tests exact equality in if and while statements or logical expressions using && or ||.
Usage (R Documentation):
identical(x, y, num.eq = TRUE, single.NA = TRUE, attrib.as.set = TRUE, ignore.bytecode = TRUE, ignore.environment = FALSE, ignore.srcref = TRUE)
References
Graphs created on Desmos.com.
R Documentation. identical. Retrieved November 10, 2020 from: https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/identical