Contents:
- What is absolute value?
- The absolute value function: Domain & Range
- Absolutely Integrable (Summable)
What is Absolute Value?
The absolute value is a number’s positive distance from zero on the number line. As it is a positive distance, absolute value can’t ever be negative.
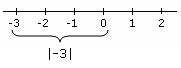
Magnitude
The absolute value also refers to the magnitude of a number. You can easily figure out the magnitude of any number by removing the negative sign. For example, the absolute value of -10 is 10 and -1000 is 1000.
Absolute value of a number is sometimes called the “modulus” of a number and is denoted by vertical bars on each side of the number. For example:
- |-10| = the abs. value of 10 = 10
- |-3| = 3
- |-22| = 22
Absolute Difference
Absolute difference, |x-y,| is the distance of two numbers on the number line. For example the absolute difference of -5 and 4 is 9:
- |-5 – 4| = 9
- |-22 – 1| = 23
- |4 – -2| = 6
(If you ever wondered why “two negatives equal a positive” in algebra, this last example, 4 – -2 helps to explain why!).
History
According to Math Boys, the word absolute comes from a variant of the word absolve and has a meaning close to free from conditions or restriction. The term, as it relates to mathematics, was first found in 1950 in the elements of analytical geometry; comprehending the doctrine of the conic sections, and the general theory of curves and surfaces of the second order by John Radford Young (1799-1885). “we have AF the positive value of x equal to BA – BF, and for the negative value, BF must exceed BA, that is, F must be on the other side of A, as at F’, hence making AF’ equal to the absolute value of the negative root of the equation”.”
What is an Absolute Value Function?
Watch the video for a how to on finding the domain and range:
An absolute value function has an expression within absolute value symbols. For example, all of the following are absolute value functions:
- y = |x|
- y = |x + 5|
- y = |x – 10| + 9
Some authors take the term “absolute value function” to mean just the first function (y = |x|). Others use it to mean all functions that include an absolute value expression. The differing terminology may stem from the fact that other functions (e.g. items 2 & 3) are just transformations (shifts and stretches) of the original function y = |x|. Therefore, y = |x| is sometimes called the “absolute value parent function.” Check with your particular author (or your instructor) to make sure you know which terminology they are using.
Absolute Value Parent Function
An absolute value function has a unique “V” shape when plotted on a graph. This is due to the fact that the absolute value of a negative number makes that number positive.
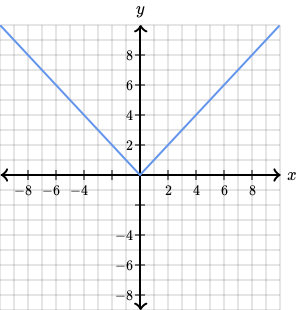
The absolute value parent function is written as:
f(x) = │x│ where:
- f(x) = x if x > 0
- 0 if x = 0
- -x if x < 0
As the definition has three pieces, this is also a type of piecewise function.
It’s only true that the absolute value function will hit (0,0) for this very specific case. Many functions you will come across in calculus will differ in where on the coordinate plane they appear. For example:
Example of Graphing an Absolute Value Function
Graph the following function using a table of values:
y = │x + 2│
Before choosing values for x, remember to include negative values for x.
| x | y =│x + 2│ |
| -5 | -5 + 2 = 3 |
| -3 | -3 + 2 = 1 |
| -2 | -2 + 2 = 0 |
| 0 | 0 + 2 = 2 |
| 2 | 2 + 2 = 4 |
| 5 | 5 + 2 = 7 |
If you were to plot the points above you would see that we end up with a “V” shaped plotted line identical to the absolute value parent function above, albeit with the vertex located at (-2, 0).
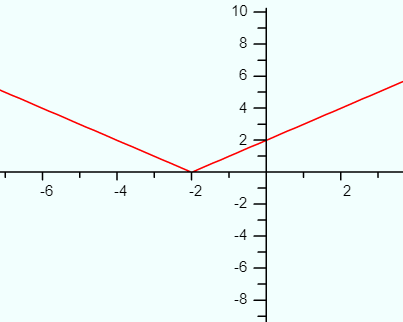
Notice also that you could have used any values for x, provided you included negative values; You would have ended up with the same result.
Absolutely Integrable
An absolutely integrable function (also called a summable function) has an integrable absolute value. “Integrable” means that you can find an integral. The “Absolutely” portion of the term refers to the fact that it’s the absolute value of the function that must be integrable on the real line (Feeman, 2015).
In notation, we can write that as:
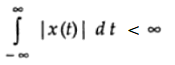
On the other hand, a function that isn’t absolutely integrable has an infinite value for the integral. It’s written in notation as:
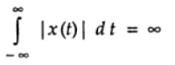
Riemann Integral vs. Absolute
A Riemann integral is the “classic” integral you’re introduced to in introductory calculus classes. Normally shortened to just “integral”, it implies that you can find the limit of an infinite number of tiny rectangles below a curve (a.k.a. Riemann sums). Absolute integration has a more rigid requirement: in addition to being able to find an integral, you must also be able to find the integral for the absolute values of the function.
Absolutely Integrable Functions in Signal Processing
Absolutely integrable functions have special importance in signal processing, because absolutely integrable continuous time or discrete time signals are stable and have Fourier transforms. Any signal generated in a lab is going to have these properties. If a signal isn’t absolutely integrable, then you can’t perform Fourier analysis.
The “severe restriction” of absolute integrability means that many useful periodic functions like sin t and cos t are not absolutely integrable and do not have Fourier transforms (Dettman, 2012). However, they can be defined on an interval of one time period (e.g. -T/2, T/2) to enable expression by a Fourier series. An alternative is to analyze the signals or functions with Laplace transform (which converts a real-valued function (like time) to a complex-valued function).
Absolutely Integrable Function Defined on an Interval
Many times, you’ll deal with functions that aren’t absolutely integrable on their entire domain. However, the condition can be defined in terms of intervals. For example, take some function f, defined on the open interval (a,b). If the function is locally integrable (i.e. the function can be integrated on the defined interval)and |f| is improperly integrable on the same interval, then the function is absolutely integrable.
An integrable function, defined on a closed interval [a. b], has an indefinite integral defined by (Mendoza, 2017):
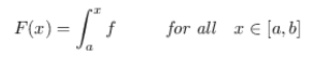 .
.
This indefinite integral is continuous and differentiable almost everywhere.
References
Dettman, J. Applied Complex Variables. Dover Publications. 2012.
Feeman, T. The Mathematics of Medical Imaging, Springer Undergraduate Texts in Mathematics and Technology, DOI 10.1007/978-3-319-22665-1
Hazelwinkel, M. Encyclopaedia of Mathematics (set). 1994. Kluwer.
Mendoza, J. Which Integrable Functions Fail to be Absolutely Integrable? Real Analysis Exchange. Vol. 43 (1), 2017. pp. 243-248.
Purdue University. Signal Properties.