Map (Mathematics)

Calculus Definitions >

Generally speaking, a map usually refers to the way a function moves a point from one place to another.

For example, imagine the Cartesian plane is a treasure map, with the coordinate point (-2, -2) marking the location of the buried loot. Worrying that someone might have discovered the treasure, we move it (or “map” it) to a new location at (2, 2). We can use a function y = |x| to describe this movement.

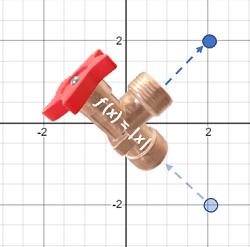
Any point can be mapped from one place to another, using a function.

A More Formal Definition of Map

More formally, map (also called mapping or transformation) is a way to assign an object in one set to another object, which could be in the same set or a different set. The “set” could be real numbers, complex numbers, or any other collection of objects. For example The function f(x) = |2| defines a mapping of a number to the absolute value of that number.

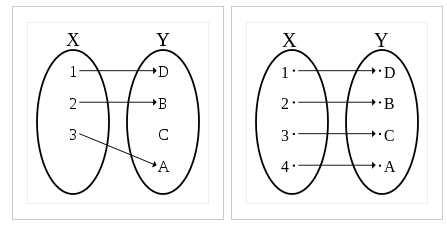
Special Classes of Maps

There are many special classes of maps, most of which also have their own subclasses. They include:

• Homomorphisms: Arise when one group is a subgroup or quotient of another group. From the Greek homo (same) and morph (shape) [1].
• Isometries: Distance preserving maps (isometry means “equal distance”. For example, f(x) = x + 3 is an isometry of the real line; the entire line is shifted by 3 but distances between points remain the same [2].
• Isomorphisms: A subclass of homomorphisms that are both injective and surjective.
• Operators: In mathematical analysis, an operator indicates a specific operation. For example, the differential operator indicates differentiation and the integral operator indicates integration.

References

[1] Macauley, M. Lecture 4.1 Homomorphisms and isomorphisms. Retrieved April 24, 2021 from: http://www.math.clemson.edu/~macaule/classes/m20_math4120/slides/math4120_lecture-4-01_h.pdf
[2] Symmetries and Isometries. Retrieved April 24, 2021 from: http://pi.math.cornell.edu/~mec/2008-2009/Victor/part1.htm