A square integrable function, also called a quadratically integrable function or Class L2 function, is defined as one where the integral of the square of the absolute value is finite (i.e. it can be calculated) for some stated interval.
For example, on the real line for the interval (-∞, +∞) a square-integrable function can be written as:
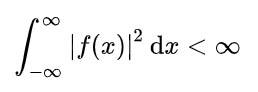
.
Examples:
- 1/xn, defined on the interval (0,1) for n < ½
- All bounded functions, defined on the interval [0, 1],
- 1/x, defined on the interval [1, ∞).
Why are Square Integrable Functions Important?
Square integrable functions make it simpler to work with certain systems and processes. Many functions in classical and quantum sciences, like wave amplitudes, are square integrable.
As an example, the quantum state of a particle is, at a given instant, defined by a wave function φ(r); Wave functions must satisfy several requirements, including being single-valued and nowhere infinite; for bound states, the function also has to be square integrable (Lowe, 2012). In addition, the wave function can’t be normalized unless it is square integrable (Greiner, 2012), i.e. if the improper integral
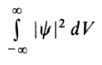
converges as follows, where M is a real constant:
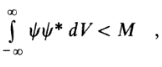
Some areas, like quantum mechanics of molecular structure, deal almost exclusively with normalizable or square integrable functions (Anderson, 2012).
References
Anderson, J. (2012). Mathematics for Quantum Chemistry. Courier Corporation.
Greiner, W. (2012). Quantum Mechanics: An Introduction. Springer Science & Business Media.
Lowe, J. (2012). Quantum Chemistry. Elsevier.
Sansone, G. “Integrable Functions.” §1.1 in Orthogonal Functions, rev. English ed. New York: Dover, pp. 1-2, 1991.
Lp Functions. Retrieved February 21, 2020 from: http://faculty.bard.edu/belk/math461/LpFunctions.pdf