A pole (also called an isolated singularity) is a point where the limit of a complex function inflates dramatically with polynomial growth.
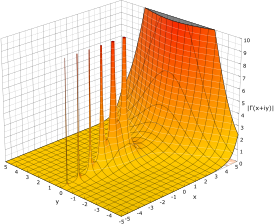
Graph of a Pole
The following graph of the absolute value of the gamma function shows several poles:
A More Precise Definition
More specifically, a point z0 is a pole of a complex-valued function f if the function value f(z) tends to infinity as z gets closer to z0. If the limit does exist, then the point is not a pole (it is a removable singularity).
A simple example is the complex reciprocal function 1/z, which has a pole at z = 0. Any function of the form f(z) = zn has a pole of order n at z = 0.
Order
Z0 is a pole of order n if:
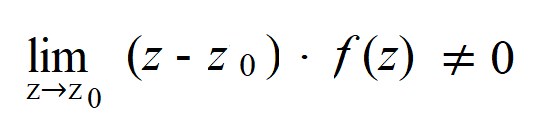
What we’re doing here is multiplying the function f(z) by (z – z0)n and then taking the limit as z approaches z0(z → z0). If the result is not equal to zero, then you have a pole.
A slightly different way to think about this is with a Laurent series. A Laurent series is a representation of the function as a power series, including negative degree terms.
A punctured disk*, 0 < |z – z0 | < can be written in terms of a Laurent series. Let’s say the series is:
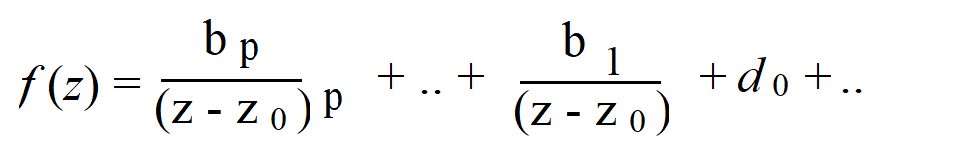
Then we can say that z0 is a pole of order p.
*A punctured disk is a disk of radius r, with a central point a. An open disk is made up of a set of complex numbers less than r, while a punctured disk is the same disc, but with a removed. You can think of it as a disk with a pinprick in the center (a pinprick that only removes the exact center, a).
References
Image: https://math.wikia.org/wiki/p o l e CC-BY-SA
Fontaine, F. (2011). Complex Numbers. Retrieved December 20, 2019 from: https://engfac.cooper.edu/pages/fred/uploads/complex0.pdf