What is a Position Function?
The position function (also called a position equation) tells you where an object is at a certain point in time. For example, the following graph of a position function tells you (in meters) where a car will be in the first few seconds after its start:
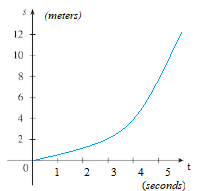
An object’s position is always relative to a location. In the above example, the car’s position at any point in time is relative to the car’s starting point.
Watch the video for an overview of the position function and how it relates to velocity and acceleration:
Velocity vs. Position in Calculus
Taking the derivative of the position function gives you the velocity of an object moving in a straight line, assuming there isn’t any air resistance. To put this another way, the velocity of an object is the rate of change of an object’s position, with respect to time.
Let’s say an object has a position function f = s(t), where:
- s = position (e.g. feet, meters, miles)
- t = time (e.g. seconds, minutes, days)
then the velocity function is v(t) = s′(t). The single prime (′) indicates the derivative (see calculus symbols).
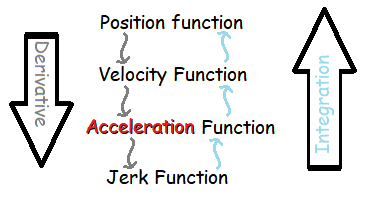
Acceleration and the Position Function
You can take this one step further: taking the derivative of the velocity function gives you the acceleration function. If you want to find acceleration from a position function, then take the derivative twice (i.e. find the second derivative).
Example question: The height of a ball thrown upwards from the top floor of a 1000 foot tall skyscraper is given by the function:
s = -16t2 + 48t + 1000
- Find the acceleration function.
- What is the acceleration of the ball at 5 seconds?
Answers:
- You’re given the position. To find acceleration, take the second derivative.
- First derivative: ds/ dt = -32t + 1000
- Second derivative: d2s/ d2t = -32
- The acceleration function is -32, so the acceleration at 5 seconds is -32.
References
Muvdi, D. et al. (1997). Dynamics for Engineers. Springer Science & Business Media/
Larson, R. (2007). Brief Calculus: An Applied Approach. Cengage Learning.
Stewart, J. (2009). Calculus: Concepts and Contexts. Cengage Learning.